
【题目】已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,﹣3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1= ![]() ,直线AC解析式为y2=ax+b.
,直线AC解析式为y2=ax+b.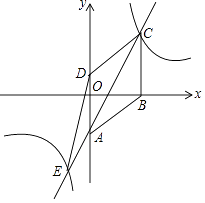
(1)求反比例函数解析式;
(2)当y1<y2时,求x的取值范围;
(3)求△CDE的面积.
【答案】
(1)解:∵A(0,﹣3),B(4,0),
∴AB= ![]() =5=BC,
=5=BC,
∴C(4,5),
∵反比例函数y1= ![]() 图象经过点C,
图象经过点C,
∴k=4×5=20,
∴反比例函数解析式为y1= ![]()
(2)解:把A(0,﹣3),C(4,5)代入y2=ax+b得,
![]() ,解得
,解得 ![]()
直线AC解析式为y2=2x﹣3,
解 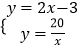 得
得 ![]() ,
,  ,
,
∴E(﹣ ![]() ,﹣8)
,﹣8)
当y1<y2时,x>4或﹣ ![]() <x<0
<x<0
(3)解:S△CDE=S△ADE+S△ADC= ![]() ××
×× ![]() +
+ ![]() ×5×4=
×5×4= ![]()
【解析】抓住已知菱形四边形ABCD是菱形,AD在y轴上,得出CB⊥x轴,根据点A、B的坐标求出菱形的边长,就可以求出点C的坐标,用待定系数法就可以求出反比例函数的解析式。
(2)先求出直线AC的函数解析式,再求出交点E的坐标,观察被直线x=-![]() 、直线x=4,、y轴分得的四部分函数图像,即可得出1<y2时,x的取值范围。
、直线x=4,、y轴分得的四部分函数图像,即可得出1<y2时,x的取值范围。
(3)根据S△CDE=S△ADE+S△ADC,根据三角形的面积公式即可求解。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】补全解答过程:
已知:如图,直线![]() ,直线
,直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ;
;![]() 平分
平分![]() ,
,![]() .求
.求![]() 的度数.
的度数.

解:![]() 与
与![]() 交于点
交于点![]() ,(已知)
,(已知)
![]() .(_______________)
.(_______________)
![]() ,(已知)
,(已知)
![]() .(______________)
.(______________)
![]() ,
,![]() 与
与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,(已知)
,(已知)
![]() (_____________)
(_____________)
![]() _______
_______![]()
![]() 平分
平分![]() ,(已知)
,(已知)
![]() _______
_______![]() .(角平分线的定义)
.(角平分线的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,问A型节能灯最多可以买多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.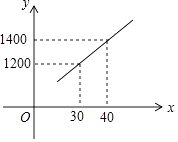
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣2a3b(﹣4a2b)÷6a4b2
(2)![]()
(3)![]()
(4)(2a﹣1)(a﹣4)﹣(a+3)(a﹣4)
(5)(x﹣3y+4)(x+3y﹣4)
(6)(a+2b)(a﹣2b)(a2﹣4b2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为4,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S10的值为 . 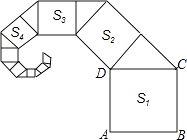
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年两会提出:随着城镇化水平的提高,为了房地产去库存,国家鼓励农民进城买房,可享受政府担保免收利息的惠民政策,小王家购买了一套学区房,首付15万元后,剩余部分贷款,贷款金额按月分期还款,每月还款数相同,计划每月还款y万元,x个月还清贷款,已知y是x的反比例函数,其图象如图所示.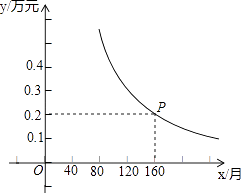
(1)求y与x的函数解析式(关系式),并求小王家购买的学区房的总价是多少万元?
(2)若计划80个月还清贷款,则每月应还款多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com