
”¾ĢāÄæ”æ(±¾ĢāĀś·Ö9·Ö)
ĮõĪĄĶ¬Ń§ŌŚŅ»“ĪæĪĶā»ī¶ÆÖŠ£¬ÓĆÓ²Ö½Ę¬×öĮĖĮ½øöÖ±½ĒČż½ĒŠĪ£¬¼ūĶ¼¢Ł”¢¢Ś£®Ķ¼¢ŁÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £»Ķ¼¢ŚÖŠ£¬
£»Ķ¼¢ŚÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £®Ķ¼¢ŪŹĒĮõĪĄĶ¬Ń§Ėł×öµÄŅ»øöŹµŃé£ŗĖū½«
£®Ķ¼¢ŪŹĒĮõĪĄĶ¬Ń§Ėł×öµÄŅ»øöŹµŃé£ŗĖū½«![]() µÄÖ±½Ē±ß
µÄÖ±½Ē±ß![]() Óė
Óė![]() µÄŠ±±ß
µÄŠ±±ß![]() ÖŲŗĻŌŚŅ»Ęš£¬²¢½«
ÖŲŗĻŌŚŅ»Ęš£¬²¢½«![]() ŃŲ
ŃŲ![]() ·½ĻņŅĘ¶Æ£®ŌŚŅĘ¶Æ¹ż³ĢÖŠ£¬
·½ĻņŅĘ¶Æ£®ŌŚŅĘ¶Æ¹ż³ĢÖŠ£¬![]() ”¢
”¢![]() Į½µćŹ¼ÖÕŌŚ
Į½µćŹ¼ÖÕŌŚ![]() ±ßÉĻ(ŅʶÆæŖŹ¼Ź±µć
±ßÉĻ(ŅʶÆæŖŹ¼Ź±µć![]() Óėµć
Óėµć![]() ÖŲŗĻ)£®
ÖŲŗĻ)£®
(1)ŌŚ![]() ŃŲ
ŃŲ![]() ·½ĻņŅĘ¶ÆµÄ¹ż³ĢÖŠ£¬ĮõĪĄĶ¬Ń§·¢ĻÖ£ŗ
·½ĻņŅĘ¶ÆµÄ¹ż³ĢÖŠ£¬ĮõĪĄĶ¬Ń§·¢ĻÖ£ŗ![]() ”¢
”¢![]() Į½µć¼äµÄ¾ąĄėÖš½„ ”ų £®
Į½µć¼äµÄ¾ąĄėÖš½„ ”ų £®
(Ģī”°²»±ä”±”¢”°±ä“ó”±»ņ”°±äŠ””±)
(2)ĮõĪĄĶ¬Ń§¾¹ż½ųŅ»²½µŲŃŠ¾æ£¬±ąÖĘĮĖČēĻĀĪŹĢā£ŗ
ĪŹĢā¢Ł£ŗµ±![]() ŅʶÆÖĮŹ²Ć“Ī»ÖĆ£¬¼“
ŅʶÆÖĮŹ²Ć“Ī»ÖĆ£¬¼“![]() µÄ³¤ĪŖ¶ąÉŁŹ±£¬
µÄ³¤ĪŖ¶ąÉŁŹ±£¬![]() ”¢
”¢![]() µÄĮ¬ĻßÓė
µÄĮ¬ĻßÓė![]() Ę½ŠŠ?
Ę½ŠŠ?
ĪŹĢā¢Ś£ŗµ±![]() ŅʶÆÖĮŹ²Ć“Ī»ÖĆ£¬¼“
ŅʶÆÖĮŹ²Ć“Ī»ÖĆ£¬¼“![]() µÄ³¤ĪŖ¶ąÉŁŹ±£¬ŅŌĻ߶Ī
µÄ³¤ĪŖ¶ąÉŁŹ±£¬ŅŌĻ߶Ī![]() ”¢
Ӣ![]() Ӣ
”¢![]() µÄ³¤¶ČĪŖČż±ß³¤µÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ?
µÄ³¤¶ČĪŖČż±ß³¤µÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ?
ĪŹĢā¢Ū£ŗŌŚ![]() µÄŅĘ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³øöĪ»ÖĆ£¬Ź¹µĆ
µÄŅĘ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³øöĪ»ÖĆ£¬Ź¹µĆ![]() ?Čē¹ū“ęŌŚ£¬
?Čē¹ū“ęŌŚ£¬
Ēó³ö![]() µÄ³¤¶Č£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ³¤¶Č£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
ĒėÄć·Ö±šĶź³ÉÉĻŹöČżøöĪŹĢāµÄ½ā“š¹ż³Ģ£®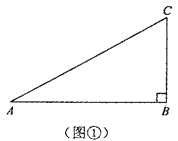
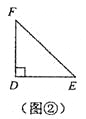
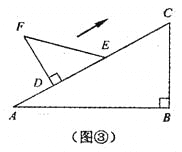
”¾“š°ø”æ£Ø1£©±äŠ”
£Ø2£©
¢Ł![]() cmŹ±£¬
cmŹ±£¬![]()
¢Śµ±![]() Ź±£¬ŅŌĻ߶Ī
Ź±£¬ŅŌĻ߶Ī![]() ”¢
Ӣ![]() Ӣ
”¢![]() µÄ³¤¶ČĪŖČż±ß³¤µÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ
µÄ³¤¶ČĪŖČż±ß³¤µÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ
¢Ū²»“ęŌŚÕāŃłµÄĪ»ÖĆ£¬Ź¹µĆ![]()
”¾½āĪö”æ
£Ø1£©±äŠ”
£Ø2£©ĪŹĢā¢Ł£ŗ½ā£ŗ”ß![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
”ą![]() .
.
ӧ![]() ,
,![]() ,
,
”ą![]() .
.
Į¬½į![]() £¬Éč
£¬Éč![]() .
.
”ą![]() ,ŌŚ
,ŌŚ![]() ÖŠ£¬DC=4.
ÖŠ£¬DC=4.
”ą![]() =12-4.
=12-4.
¼“![]() cmŹ±£¬
cmŹ±£¬![]()
ĪŹĢā¢Ś£ŗ½ā£ŗÉčµ±![]() £¬
£¬
ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() .
.
£Ø¢ń£©µ±![]() ĪŖŠ±±ßŹ±£¬ÓÉ
ĪŖŠ±±ßŹ±£¬ÓÉ![]() µĆ£¬
µĆ£¬![]() ,
,![]() .
.
(¢ņ)µ±![]() ĪŖŠ±±ßŹ±£¬ÓÉ
ĪŖŠ±±ßŹ±£¬ÓÉ![]() µĆ£¬
µĆ£¬![]() ,
,![]() £Ø²»·ūŗĻĢāŅā£¬ÉįČ„£©.
£Ø²»·ūŗĻĢāŅā£¬ÉįČ„£©.
(¢ó)µ±![]() ĪŖŠ±±ßŹ±£¬ÓÉ
ĪŖŠ±±ßŹ±£¬ÓÉ![]() µĆ£¬
µĆ£¬![]() ,
,![]() ,
,
![]() =144-248<0,
=144-248<0,
”ą·½³ĢĪŽ½ā.
”ąÓÉ(¢ń)”¢(¢ņ)”¢(¢ó)µĆ£¬
µ±![]() Ź±£¬ŅŌĻ߶Ī
Ź±£¬ŅŌĻ߶Ī![]() ”¢
Ӣ![]() Ӣ
”¢![]() µÄ³¤¶ČĪŖČż±ß³¤µÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ.
µÄ³¤¶ČĪŖČż±ß³¤µÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ.
ĪŹĢā¢Ū²»“ęŌŚÕāŃłµÄĪ»ÖĆ£¬Ź¹µĆ![]() .
.
¼ŁÉč![]() £¬ÓÉ
£¬ÓÉ![]() ,µĆ
,µĆ![]() .×÷
.×÷![]() µÄĘ½·ÖĻߣ¬½»
µÄĘ½·ÖĻߣ¬½»![]() ÓŚ
ÓŚ![]() ,
,
Ōņ![]() ,
,
”ą![]() .
.
”ą![]() ,
,![]() .
.
”ą![]() .
.
”ą²»“ęŌŚÕāŃłµÄĪ»ÖĆ£¬Ź¹µĆ![]() .
.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
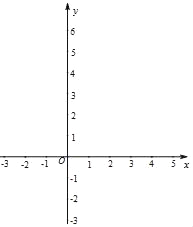
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßy=ax2©4ax+3a£Øa£¾0£©ÓėxÖį½»ÓŚA£¬BĮ½µć£ØAŌŚBµÄ×ó²ą£©£®
£Ø1£©ĒóÅ×ĪļĻߵĶŌ³ĘÖį¼°µćA£¬BµÄ×ų±ź£»
£Ø2£©µćC£Øt£¬3£©ŹĒÅ×ĪļĻßy=ax2©4ax+3a£Øa£¾0£©ÉĻŅ»µć£¬£ØµćCŌŚ¶Ō³ĘÖįµÄÓŅ²ą£©£¬¹żµćC×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖµćD£®
¢Łµ±CD=ADŹ±£¬Ēó“ĖŹ±Å×ĪļĻߵıķ“ļŹ½£»
¢Śµ±CD£¾ADŹ±£¬ĒótµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
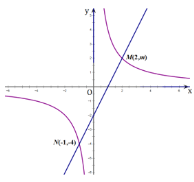
”¾ĢāÄæ”æŅ»“ĪŗÆŹż![]() Ķ¼ĻóÓė·“±ČĄżŗÆŹż
Ķ¼ĻóÓė·“±ČĄżŗÆŹż![]() µÄĶ¼Ļó½»ÓŚµćM”¢N.
µÄĶ¼Ļó½»ÓŚµćM”¢N.
£Ø1£©ĒóÕāĮ½øöŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©øł¾ŻĶ¼Ļ󊓳öŹ¹![]() µÄ×Ō±äĮæµÄȔֵ·¶Ī§.
µÄ×Ō±äĮæµÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£×éÖÆѧɜŹé·Ø±ČČü£¬¶Ō²ĪČü×÷Ę·°“A”¢B”¢C”¢DĖÄøöµČ¼¶½ųŠŠĮĖĘĄ¶Ø£®ĻÖĖ껜Ȕ²æ·ÖѧɜŹé·Ø×÷Ę·µÄĘĄ¶Ø½į¹ū½ųŠŠ·ÖĪö£¬²¢»ęÖĘÉČŠĪĶ³¼ĘĶ¼ŗĶĢõŠĪĶ³¼ĘĶ¼ČēĻĀ£ŗ

øł¾ŻÉĻŹöŠÅĻ¢Ķź³ÉĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒóÕā“Ī³éČ”µÄŃł±¾µÄČŻĮ棻
£Ø2£©ĒėŌŚĶ¼¢ŚÖŠ°ŃĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©ŅŃÖŖøĆŠ£Õā“Ī»ī¶Æ¹²ŹÕµ½²ĪČü×÷Ę·750·Ż£¬ĒėÄć¹Ą¼Ę²ĪČü×÷Ę·“ļµ½B¼¶ŅŌÉĻ£Ø¼“A¼¶ŗĶB¼¶£©ÓŠ¶ąÉŁ·Ż£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µćPµÄ×ų±źĪŖ£Øx1£¬y1£©£¬µćQµÄ×ų±źĪŖ£Øx2£¬y2£©£¬ĒŅx1”Łx2£¬y1”Ły2£®ČōP£¬QĪŖijøö¾ŲŠĪµÄĮ½øö¶„µć£¬ĒŅøĆ¾ŲŠĪµÄ±ß¾łÓėijĢõ×ų±źÖį“¹Ö±£¬Ōņ³ĘøĆ¾ŲŠĪĪŖµćP£¬QµÄ”°Ļą¹Ų¾ŲŠĪ”±£¬ĻĀĶ¼¢ŁĪŖµćP£¬QµÄ”°Ļą¹Ų¾ŲŠĪ”±µÄŹ¾ŅāĶ¼£®
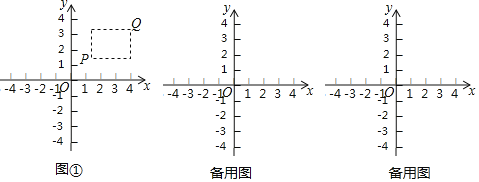
ŅŃÖŖµćAµÄ×ų±źĪŖ£Ø1£¬0£©£¬
£Ø1£©ČōµćBµÄ×ų±źĪŖ£Ø3£¬1£©£¬ĒóµćA£¬BµÄ”°Ļą¹Ų¾ŲŠĪ”±µÄĆ껿£»
£Ø2£©µćCŌŚÖ±Ļßx£½3ÉĻ£¬ČōµćA£¬CµÄ”°Ļą¹Ų¾ŲŠĪ”±ĪŖÕż·½ŠĪ£¬ĒóÖ±ĻßACµÄ±ķ“ļŹ½£»
£Ø3£©ČōµćDµÄ×ų±źĪŖ£Ø4£¬2£©£¬½«Ö±Ļßy£½2x+bĘ½ŅĘ£¬µ±ĖüÓėµćA£¬DµÄ”°Ļą¹Ų¾ŲŠĪ”±Ć»ÓŠ¹«¹²µćŹ±£¬Ēó³öbµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĻģÓ¦½š»ŖŹŠÕžø®·¢³öµÄ““ĪÄĆ÷³ĒŹŠŗÅÕŁ£¬Ń§Š£×ÜĪń“¦ĮõĄĻŹ¦ÓĆMŌŖ¹ŗĀņ»Ø»Ü·¢øųø÷°ąĆĄ»ÆĪĄÉś±£½ąĒų.ČōŅŌ2æĆŹ÷ŗĶ3Öź»ØĪŖŅ»·Ż£¬ŌņæÉŅŌĀņ60·Ż£»ČōŅŌ2æĆŹ÷ŗĶ6Öź»ØĪŖŅ»·Ż£¬ŌņæÉŅŌĀņ40·Ż.ÉčŹ÷µÄµ„¼ŪĪŖxŌŖ/æĆ£¬»ØµÄµ„¼ŪĪŖyŌŖ/Öź.
(1)µ±![]() Ź±£¬ĒóŹ÷ŗĶ»ØµÄµ„¼Ū.
Ź±£¬ĒóŹ÷ŗĶ»ØµÄµ„¼Ū.
(2)ČōÓĆÕāMŌŖČ«²æ¹ŗĀņ»Ø£¬×ܹ²æÉŅŌĀņ¼øÖź»Ø?
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬AB£½![]() £¬AD£½2£®µćEŹĒBC±ßÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓAE£¬¹żµćD×÷DF”ĶAEÓŚµćF£®µ±”÷CDFŹĒµČŃüČż½ĒŠĪŹ±£¬BEµÄ³¤ĪŖ_____£®
£¬AD£½2£®µćEŹĒBC±ßÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓAE£¬¹żµćD×÷DF”ĶAEÓŚµćF£®µ±”÷CDFŹĒµČŃüČż½ĒŠĪŹ±£¬BEµÄ³¤ĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”潚ĢĆĘļ×ŌŠŠ³µĀĆŠŠŌ½Ą“Ō½ŹÜµ½ČĖĆĒµÄĻ²°®£¬ø÷ÖÖĘ·ÅʵÄɽµŲ×ŌŠŠ³µĻą¼ĢĶ¶·ÅŹŠ³”£¬Ä³³µŠŠ¾ÓŖµÄAŠĶ³µČ„Äź2ŌĀ·ŻĻśŹŪ×ܶīĪŖ3.2ĶņŌŖ£¬½ńÄź¾¹żøÄŌģÉż¼¶ŗóAŠĶ³µĆæĮ¾ĻśŹŪ¼Ū±ČČ„ÄźŌö¼Ó400ŌŖ£¬Čō½ńÄź2ŌĀ·ŻÓėČ„Äź2ŌĀ·ŻĀō³öµÄAŠĶ³µŹżĮæĻąĶ¬£¬Ōņ½ńÄź2ŌĀ·ŻAŠĶ³µĻśŹŪ×ܶī½«±ČČ„Äź2ŌĀ·ŻĻśŹŪ×ܶīŌö¼Ó25%£®
£Ø1£©Ēó½ńÄź2ŌĀ·ŻAŠĶ³µĆæĮ¾ĻśŹŪ¼Ū¶ąÉŁŌŖ£æ
£Ø2£©øĆ³µŠŠ¼Ę»®½ńÄź3ŌĀ·ŻŠĀ½ųŅ»ÅśAŠĶ³µŗĶBŠĶ³µ¹²50Į¾£¬ĒŅBŠĶ³µµÄ½ų»õŹżĮæ²»³¬¹żAŠĶ³µŹżĮæµÄ2±¶£¬A”¢BĮ½ÖÖŠĶŗųµµÄ½ų»õŗĶĻśŹŪ¼ŪøńČēĻĀ±ķ£¬ĪŹÓ¦ČēŗĪ½ų»õ²ÅÄÜŹ¹ÕāÅś³µ»ńĄū×ī¶ą£æ””

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼Ņ»£¬Å×ĪļĻßy=ax2+bx+cÓėxÖįÕż°ėÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬Ö±Ļßy=x-2¾¹żA”¢CĮ½µć£¬ĒŅAB=2£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ČōÖ±ĻßDEĘ½ŠŠÓŚxÖį²¢“ÓCµćæŖŹ¼ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲyÖįÕż·½ĻņĘ½ŅĘ£¬ĒŅ·Ö±š½»yÖį”¢Ļ߶ĪBCÓŚµćE£¬D£¬Ķ¬Ź±¶ÆµćP“ÓµćB³ö·¢£¬ŃŲBO·½ĻņŅŌĆæĆė2øöµ„Ī»ĖŁ¶ČŌĖ¶Æ£¬£ØČēĶ¼2£©£»µ±µćPŌĖ¶Æµ½ŌµćOŹ±£¬Ö±ĻßDEÓėµćP¶¼Ķ£Ö¹ŌĖ¶Æ£¬Į¬DP£¬ČōµćPŌĖ¶ÆŹ±¼äĪŖtĆė£»Éčs=![]() £¬µ±tĪŖŗĪÖµŹ±£¬sÓŠ×īŠ”Öµ£¬²¢Ēó³ö×īŠ”Öµ£®
£¬µ±tĪŖŗĪÖµŹ±£¬sÓŠ×īŠ”Öµ£¬²¢Ēó³ö×īŠ”Öµ£®
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ŹĒ·ń“ęŌŚtµÄÖµ£¬Ź¹ŅŌP”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£»Čō“ęŌŚ£¬ĒótµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com