
 如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号).
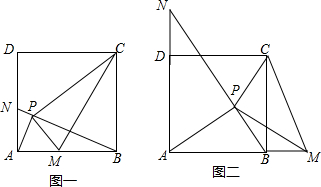
如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号). 分析 设CF=x米,则NF=x米,MF=(x+7)米,由∠CMN=30°可知tan30°=$\frac{CF}{MF}$,把NF=x米,MF=x+7米代入即可求出x的值,再根据CD=CF+EF-DE即可得出结论.
解答 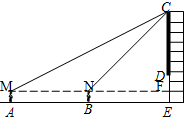 解:如图,设CF=x米,则NF=x米
解:如图,设CF=x米,则NF=x米
∵tan30°=$\frac{CF}{MF}$=$\frac{\sqrt{3}}{3}$
∴$\frac{x}{x+7}$=$\frac{\sqrt{3}}{3}$,
∴x=$\frac{7}{2}$($\sqrt{3}$+1),
∴CD=x+1.6-4=$\frac{7}{2}$$\sqrt{3}$+11.
答:电子屏幕上端与下端之间的距离CD为$\frac{7}{2}$$\sqrt{3}$+11米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,解答此类问题的关键是找出符合条件的直角三角形,利用锐角三角函数的定义进行解答.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=8}\\{xy+18=yx}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=8}\\{10(x+y)+18=yx}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=8}\\{10x+y+18=yx}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=8}\\{x+10y+18=10x+y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
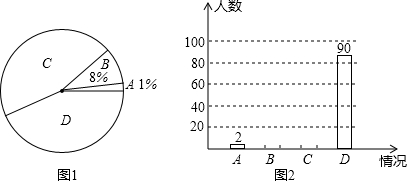
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛一枚图钉钉尖着地和钉尖朝上的概率一样大 | |
| B. | 彩票中奖的机会是1%,买100张一定会中奖 | |
| C. | 天气预报说明天下雨的概率是50%,所以明天将有一半的时间在下雨 | |
| D. | 在同一年出生的367名学生中,至少有两人的生日是同一天 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
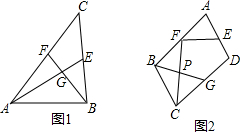
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
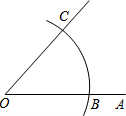 如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:| 活动次数x | 频数 | 频率 |
| 0<x≤3 | 10 | 0.20 |
| 3<x≤6 | a | 0.24 |
| 6<x≤9 | 16 | 0.32 |
| 9<x≤12 | 6 | 0.12 |
| 12<x≤15 | m | b |
| 15<x≤18 | 2 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com