
分析 (1)观察可得方程最简公分母为(2x-5),将方程去分母转化为整式方程即可求解.
(2)观察可得方程最简公分母为(x+2)(x-2),将方程去分母转化为整式方程即可求解.
解答 解:(1)$\frac{x}{2x-5}$$-\frac{5}{5-2x}$=1,
去分母得:x+5=2x-5,
移项、合并同类项得:-x=-10,
系数化为1得:x=10,
经检验x=10是原分式方程的解,
故原分式方程的解是x=10.
(2)$\frac{x+2}{x-2}$-1=$\frac{16}{{x}^{2}-4}$,
去分母得:(x+2)2-(x2-4)=16,
去括号得:x2+4x+4-x2+4=16,
移项、合并同类项得:4x=8,
系数化为1得:x=2,
经检验x=2是原分式方程增根,
故原分式方程无解.
点评 本题考查解分式方程的能力,解分式方程去分母时有常数项的注意不要漏乘,求解后要进行检验,这两项是都是容易忽略的地方,要注意检查.


科目:初中数学 来源: 题型:解答题
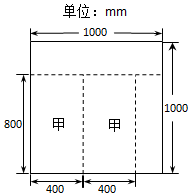 某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)
某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)| 方案一 | 方案二 | 方案三 | |
| 甲种型号瓷砖块数 | 1 | 2 | b |
| 乙种型号瓷砖块数 | a | 0 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
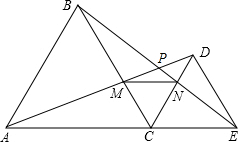 如图,点C为线段AE上任意一点,在AE同侧分别作等边三角形△ABC和等边三角形△CDE,连接AD,BE分别交BC,CD于点M,N,连接MN,则下列结论:
如图,点C为线段AE上任意一点,在AE同侧分别作等边三角形△ABC和等边三角形△CDE,连接AD,BE分别交BC,CD于点M,N,连接MN,则下列结论:| A. | ①②③④⑤ | B. | ①③④⑤ | C. | ①②④⑤ | D. | ①②③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
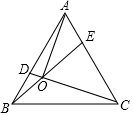 如图,点D、E分别是等边△ABC的边AB、AC上的点,满足BD=AE,连结CD、BE交于点O.已知BO=2,CO=5,则AO的长为( )
如图,点D、E分别是等边△ABC的边AB、AC上的点,满足BD=AE,连结CD、BE交于点O.已知BO=2,CO=5,则AO的长为( )| A. | 3 | B. | $\sqrt{21}$ | C. | 4 | D. | $\sqrt{19}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
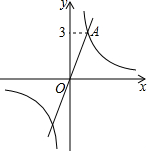 如图,在平面直角坐标系xOy中,过坐标原点O的直线l与双曲线y=$\frac{3}{x}$相交于点A(m,3).
如图,在平面直角坐标系xOy中,过坐标原点O的直线l与双曲线y=$\frac{3}{x}$相交于点A(m,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com