Question

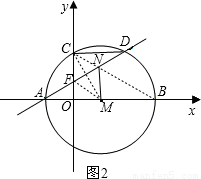
如图，⊙M的圆心M在x轴上，⊙M分别交x轴于点A、B（A在B的左边），交y轴的正半轴于点C，弦CD∥x轴交⊙M于点D，已知A、B两点的横坐标分别是方程x2=4（x+3）的两个根，

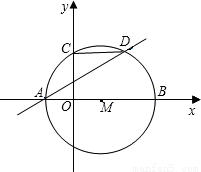
（1）求点C的坐标；

（2）求直线AD的解析式；

（3）点N是直线AD上的一个动点，求△MNB周长的最小值，并在图中画出△MNB周长最小时点N的位置．

Answer 1

（1） 点C的坐标是（0，2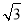）；（2） 直线AD的解析式是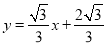；（3） .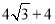

【解析】

试题分析：（1）解方程求出两个根，从而得到点A、B的坐标，然后求出点M的坐标与圆的半径，连接CM，在Rt△CMO中，利用勾股定理列式求出OC的长度，即可写出点C的坐标；

（2）过点M作ME⊥CD，根据垂径定理可得CD=2CE=2OM，然后得到点D的坐标，再根据待定系数法即可求出直线AD的解析式；

（3）找出点M关于直线AD的对称点，对称点与点B连接交AD于点N，连接MN，根据轴对称的性质，△MNB就是所要求作的周长最小的三角形，设直线AD与y轴相交于点F，连接FM，先利用直线AD的解析式求出点F的坐标，再根据勾股定理求出FM的长度，然后根据线段垂直平分线上的点到线段两端点的距离相等即可得到点M的对称点就是点C，再根据勾股定理求出BC的长度，也就是BN+MN，从而三角形的周长不难求出．

试题解析：（1）方程x2=4（x+3）整理得，

x2-4x-12=0，

即（x+2）（x-6）=0，

∴x+2=0，x-6=0，

解得x=-2，或x=6，

∴点A、B的坐标分别为：A（-2，0），B（6，0），

（-2+6）÷2=2，[6-（-2）]÷2=4，

∴点M的坐标是（2，0），⊙M的半径是4，

连接CM，则OC==，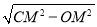

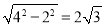∴点C的坐标是（0，2）；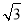

（2）如图1，过点M作ME⊥CD，

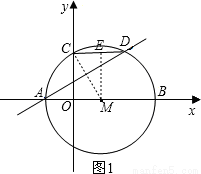
则CE=E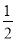D=CD，

∵CD∥x轴，

∴ME⊥x轴，

∴四边形OMEC是矩形，

∴CE=OM=2，

∴CD=4，

点D的坐标是（4，2），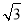

设直线AD的解析式是y=kx+b，

∴

解得

，

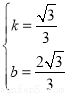∴直线AD的解析式是；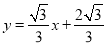

（3）如图2，设直线AD与y轴的交点是F，

当x=0时，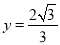

∴点F的坐标是（0，），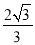

在Rt△OMF中，FM=，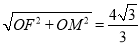

，

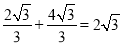∴点M关于直线AD的对称点是点C，

连接BC交直线AD于点N，连接MN，则△MNB就是所要求作的周长最小的三角形，

此时，在△OBC中，BC=，

△MNB周长=BN+CN+BM=BC+BM=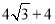

点N的位置如图2所示．

考点：一次函数综合题．