
分析 ①如图1,点E在CD的延长线上,解直角三角形得到DE=$\frac{\sqrt{3}}{3}$AD=2$\sqrt{3}$,AE=4$\sqrt{3}$,根据折叠的性质得到MN⊥AE,AF=EF=$\frac{1}{2}$AE=2$\sqrt{3}$,求得EN=4$\sqrt{3}$,于是得到结论;②如图2,点E在CD上,解直角三角形的得到DE=$\frac{\sqrt{3}}{3}$AD=2$\sqrt{3}$,求得CE=6-2$\sqrt{3}$,由折叠的性质得到MN垂直平分AE,根据线段垂直平分线的性质得到AN=EN,设CN=x,则BN=6-x,根据勾股定理列方程即可得到结论.
解答 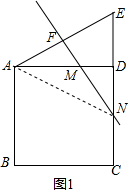 解:①如图1,点E在CD的延长线上,
解:①如图1,点E在CD的延长线上,
∵四边形ABCD 是正方形,
∴AD=6,∠ADC=∠ADE=90°,
∵∠DAE=30°,
∴∠E=60°,
∴DE=$\frac{\sqrt{3}}{3}$AD=2$\sqrt{3}$,AE=4$\sqrt{3}$,
∵折叠正方形ABCD,使点A与点E重合,
∴MN⊥AE,AF=EF=$\frac{1}{2}$AE=2$\sqrt{3}$,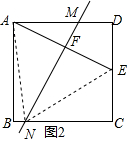
∴EN=4$\sqrt{3}$,
∴DN=4$\sqrt{3}$-2$\sqrt{3}$=2$\sqrt{3}$,
∴CN=6-2$\sqrt{3}$;
②如图2,点E在CD上,
∵四边形ABCD 是正方形,
∴AD=6,∠ADC=90°,
∵∠DAE=30°,
∴DE=$\frac{\sqrt{3}}{3}$AD=2$\sqrt{3}$,
∴CE=6-2$\sqrt{3}$,
∵折叠正方形ABCD,使点A与点E重合,
∴MN垂直平分AE,
∴AN=EN,
设CN=x,则BN=6-x,
∵AB2+BN2=AN2,CN2+CE2=EN2,
∴AB2+BN2=CN2+CE2,
即62+(6-x)2=x2+(6-2$\sqrt{3}$)2,
∴x=2+2$\sqrt{3}$,
∴CN=2+2$\sqrt{3}$.
综上所述:线段CN的长为6-2$\sqrt{3}$或2+2$\sqrt{3}$.
故答案为:6-2$\sqrt{3}$或2+2$\sqrt{3}$.
点评 本题考查了翻折变换(折叠问题),正方形的性质,线段垂直平分线的性质,勾股定理,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校小组利用暑假中前40天参加社会实践活动,参与了一家网上书店经营,了解到一种成本每本20元的书在x天销售量P=50-x.在第x天的售价每本y元,y与x的关系如图所示. 已知当社会实践活动时间超过一半后.y=20+$\frac{315}{x}$
某学校小组利用暑假中前40天参加社会实践活动,参与了一家网上书店经营,了解到一种成本每本20元的书在x天销售量P=50-x.在第x天的售价每本y元,y与x的关系如图所示. 已知当社会实践活动时间超过一半后.y=20+$\frac{315}{x}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在数轴上,点A表示的数是10,点C在原点的左侧,与点A到原点距离相等,点D在点A的左侧,与点A的距离为8个单位长度,点B到C、D两点的距离相等
如图,在数轴上,点A表示的数是10,点C在原点的左侧,与点A到原点距离相等,点D在点A的左侧,与点A的距离为8个单位长度,点B到C、D两点的距离相等查看答案和解析>>
科目:初中数学 来源: 题型:解答题
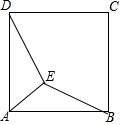 如图,点E是正方形ABCD内一点,DE=2,AE=1,EB=$\sqrt{2}$
如图,点E是正方形ABCD内一点,DE=2,AE=1,EB=$\sqrt{2}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com