
【题目】某商场进行有奖促销活动,规定顾客购物达到一定金额就可以获得一次转动转盘的机会(如图),当转盘停止转动时指针落在哪一区域就可获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“10元兑换券”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“10元兑换券”的频率 | 0.68 | a | 0.68 | 0.69 | b | 0.701 |
(1)a的值为 ,b的值为 ;
(2)假如你去转动该转盘一次,获得“10元兑换券”的概率约是 ;(结果精确到0.01)
(3)根据(2)的结果,在该转盘中表示“20元兑换券”区域的扇形的圆心角大约是多少度?(结果精确到1°)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
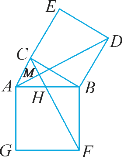
【题目】如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连接AD、CF,AD与CF交于点M,AB与CF交于点H.
(1)求证:△ABD≌△FBC;
(2)已知AD=6,求四边形AFDC的面积;
(3)在△ABC中,设BC=a,AC=b,AB=c,当∠ACB≠90°时,c![]() ≠a
≠a![]() +b
+b![]() .在任意△ABC中,c
.在任意△ABC中,c![]() =a
=a![]() +b
+b![]() +k.就a=3,b=2的情形,探究k的取值范围(只需写出你得到的结论即可).
+k.就a=3,b=2的情形,探究k的取值范围(只需写出你得到的结论即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )

A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的实验最有可能的是( )

A. 袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球
B. 掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C. 先后两次掷一枚质地均匀的硬币,两次都出现反面
D. 先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查![]() 随机调查了某班所有同学最喜欢的节目
随机调查了某班所有同学最喜欢的节目![]() 每名学生必选且只能选择四类节目中的一类
每名学生必选且只能选择四类节目中的一类![]() 并将调查结果绘成如下不完整的统计图
并将调查结果绘成如下不完整的统计图![]() 根据两图提供的信息,回答下列问题:
根据两图提供的信息,回答下列问题:
![]() 最喜欢娱乐类节目的有______人,图中
最喜欢娱乐类节目的有______人,图中![]() ______;
______;
![]() 请补全条形统计图;
请补全条形统计图;
![]() 根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;
根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;
![]() 在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.
在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com