
如图,⊿ACO的顶点A,C分别是双曲线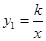 与直线
与直线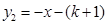 在第二象限、第四象限的交点,AB⊥
在第二象限、第四象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO=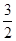
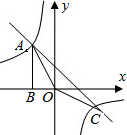
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)根据图象写出使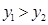 的自变量x的取值范围.
的自变量x的取值范围.
(1)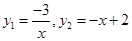 ;(2)A(-1,3),C(3,-1);(3)
;(2)A(-1,3),C(3,-1);(3)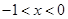 或
或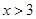
解析试题分析:(1)先根据反比例函数的图象所在的象限判断出k的符号,在由△ABO的面积求出k的值,进而可得出两个函数的解析式;
(2)把两函数的解析式组成方程组,求出x、y的值,即可得出A、C两点的坐标;
(3)直接根据一次函数与反比例函数的交点坐标求出反比例函数的值大于一次函数的值x的取值范围即可.
(1)∵反比例函数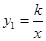 的图象在二、四象限,
的图象在二、四象限,
∴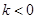
∵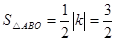
∴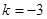
∴双曲线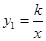 的解析式为
的解析式为
直线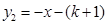 的解析式为
的解析式为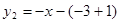 ,即
,即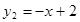 ;
;
(2)∵把一次函数与反比例函数的解析式组成方程组得: ,解得
,解得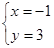 或
或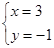
∴A(-1,3),C(3,-1);
(23)∵A(-1,3),C(3,-1),
∴当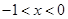 或
或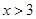 时,
时,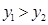 .
.
考点:反比例函数与一次函数的交点问题
点评:解答本题的关键是熟练掌握待定系数法求一次函数及反比例函数的解析式,能根据△ABO的面积求出k的值.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
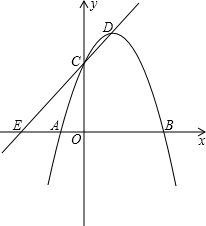 图象顶点为D,OB=OC,tan∠ACO=
图象顶点为D,OB=OC,tan∠ACO=| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
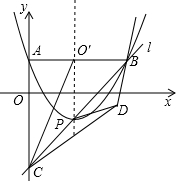 落在点D的位置.
落在点D的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ACO的顶点A,C分别是双曲线
如图,△ACO的顶点A,C分别是双曲线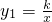 与直线y2=-x-(k+1)在第二象限、第四象限的交点,AB⊥x轴于B且S△ABO=
与直线y2=-x-(k+1)在第二象限、第四象限的交点,AB⊥x轴于B且S△ABO=
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省九年级第二次月考数学试卷(解析版) 题型:解答题
如图,⊿ACO的顶点A,C分别是双曲线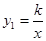 与直线
与直线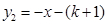 在第二象限、第四象限的交点,AB⊥
在第二象限、第四象限的交点,AB⊥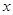 轴于B且S△ABO=
轴于B且S△ABO=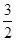
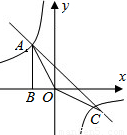
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)根据图象写出使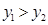 的自变量x的取值范围.
的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com