
 探究:如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和点D,直线l3有一点P
探究:如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和点D,直线l3有一点P分析 (1)当P点在C、D之间运动时,首先过点P作PE∥l1,由l1∥l2,可得PE∥l2∥l1,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD.
(2)当点P在C、D两点的外侧运动时,由直线l1∥l2,根据两直线平行,同位角相等与三角形外角的性质,即可求得:∠PBD=∠PAC+∠APB.
解答 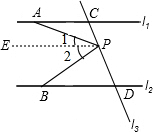 解:(1)如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
解:(1)如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;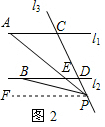
(2)如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
点评 本题主要考查平行线的性质与三角形外角的性质.此题难度适中,解题的关键是掌握:两直线平行,内错角相等与两直线平行,同位角相等,注意辅助线的作法.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
 如图所示,在一张某地区的地图上,原来标有学校,公园和广场三个位置,由于被墨水污染,广场的具体位置已看不清了,根据记忆,广场的位置在学校的北偏东60°的方向,在公园的北偏西45°的方向,根据上述信息,请找出广场的具体位置.
如图所示,在一张某地区的地图上,原来标有学校,公园和广场三个位置,由于被墨水污染,广场的具体位置已看不清了,根据记忆,广场的位置在学校的北偏东60°的方向,在公园的北偏西45°的方向,根据上述信息,请找出广场的具体位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某校调查初一年级3个班的一次数学成绩的条形图.
如图是某校调查初一年级3个班的一次数学成绩的条形图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m)2与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m)2与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )| A. | 100m2 | B. | 50m2 | C. | 80m2 | D. | 40m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com