Question

5．在平面直角坐标系中，抛物线y=ax²-5ax+4a与x轴交于A、B（A点在B点的左侧）与y轴交于点C．
（1）如图1，连接AC、BC，若△ABC的面积为3时，求抛物线的解析式；
（2）如图2，点P为第四象限抛物线上一点，连接PC，若∠BCP=2∠ABC时，求点P的横坐标；
（3）如图3，在（2）的条件下，点F在AP上，过点P作PH⊥x轴于H点，点K在PH的延长线上，AK=KF，∠KAH=∠FKH，PF=-4$\sqrt{2}$a，连接KB并延长交抛物线于点Q，求PQ的长．

Answer 1

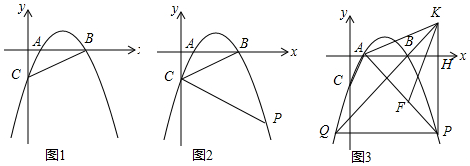
分析 （1）通过解方程ax²-5ax+4a=0可得到A（1，0），B（4，0），然后利用三角形面积公式求出OC得到C点坐标，再把C点坐标代入y=ax²-5ax+4a中求出a即可得到抛物线的解析式；
（2）过点P作PH⊥x轴于H，作CD⊥PH于点H，如图2，设P（x，ax²-5ax+4a），则PD=-ax²+5ax，通过证明Rt△PCD∽Rt△CBO，利用相似比可得到（-ax²+5ax）：（-4a）=x：4，然后解方程求出x即可得到点P的横坐标；
（3）过点F作FG⊥PK于点G，如图3，先证明∠HAP=∠KPA得到HA=HP，由于P（6，10a），则可得到-10a=6-1，解得a=-$\frac{1}{2}$，再判断Rt△PFG单位等腰直角三角形得到FG=PG=$\frac{\sqrt{2}}{2}$PF=2，接着证明△AKH≌△KFG，得到KH=FG=2，则K（6，2），然后利用待定系数法求出直线KB的解析式为y=x-4，再通过解方程组$\left\{\begin{array}{l}{y=x-4}\\{y=-\frac{1}{2}{x}^{2}+\frac{5}{2}x-2}\end{array}\right.$得到Q（-1，-5），利用P、Q点的坐标可判断PQ∥x 轴，于是可得到QP=7．

解答 解：（1）当y=0时，ax²-5ax+4a=0，解得x₁=1，x₂=4，则A（1，0），B（4，0），
∴AB=3，
∵△ABC的面积为3，
∴$\frac{1}{2}$•4•OC=3，解得OC=2，则C（0，-2），
把C（0，-2）代入y=ax²-5ax+4a得4a=-2，解得a=-$\frac{1}{2}$，
∴抛物线的解析式为y=-$\frac{1}{2}$x²+$\frac{5}{2}$x-2；
（2）过点P作PH⊥x轴于H，作CD⊥PH于点H，如图2，设P（x，ax²-5ax+4a），则PD=4a-（ax²-5ax+4a）=-ax²+5ax，
∵AB∥CD，
∴∠ABC=∠BCD，
∵∠BCP=2∠ABC，
∴∠PCD=∠ABC，
∴Rt△PCD∽Rt△CBO，
∴PD：OC=CD：OB，
即（-ax²+5ax）：（-4a）=x：4，解得x₁=0，x₂=6，
∴点P的横坐标为6；
（3）过点F作FG⊥PK于点G，如图3，
∵AK=FK，
∴∠KAF=∠KFA，
而∠KAF=∠KAH+∠PAH，∠KFA=∠PKF+∠KPF，
∵∠KAH=∠FKP，
∴∠HAP=∠KPA，
∴HA=HP，
∴△AHP为等腰直角三角形，
∵P（6，10a），
∴-10a=6-1，解得a=-$\frac{1}{2}$，
在Rt△PFG中，∵PF=-4$\sqrt{2}$a=2$\sqrt{2}$，∠FPG=45°，
∴FG=PG=$\frac{\sqrt{2}}{2}$PF=2，
在△AKH和△KFG中
$\left\{\begin{array}{l}{∠AHK=∠KGF}\\{∠KAH=GKF}\\{KA=FK}\end{array}\right.$，
∴△AKH≌△KFG，
∴KH=FG=2，
∴K（6，2），
设直线KB的解析式为y=mx+n，
把K（6，2），B（4，0）代入得$\left\{\begin{array}{l}{6k+b=2}\\{4k+b=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=1}\\{b=-4}\end{array}\right.$，
∴直线KB的解析式为y=x-4，
当a=-$\frac{1}{2}$时，抛物线的解析式为y=-$\frac{1}{2}$x²+$\frac{5}{2}$x-2，
解方程组$\left\{\begin{array}{l}{y=x-4}\\{y=-\frac{1}{2}{x}^{2}+\frac{5}{2}x-2}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=-1}\\{y=-5}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$，
∴Q（-1，-5），
而P（6，-5），
∴PQ∥x 轴，
∴QP=7．

点评 本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会利用全等三角形的知识证明线段相等和相似比计算线段的长．