Question

今有一个三位数，其各位数字不尽相同，如将此三位数的各位数字重新排列，必可得一个最大数和一个最小数（例如，427，经重新排列得最大数742，最小数247），如果所得最大数与最小数之差就是原来的那个三位数，试求这个三位数．

Answer 1

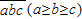
【答案】分析：首先根据题意设重排后最大数为，再由最大数与最小数之差就是原来的那个三位数与c＜a，可得关系式10+c-a=z，10+（b-1）-b=y，（a-1）-c=x，即可求得x，y，z的值，求得这个三位数．
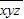
解答：解：设三位数为，重排后最大数为，
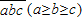
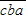
则最小数为，于是有，
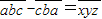
由于c＜a，
由上式有10+c-a=z，10+（b-1）-b=y，（a-1）-c=x．
可求得y=9，x=4，z=5．
即所求三位数为495．
点评：解此题的关键是理解题意，根据题意表示出各种情况下的数字，然后求得方程式．解题时要注意细心．