
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,点E是AC的一点,连接EB,过点A做AM⊥BE,垂足为M,AM与BD相交于点F.
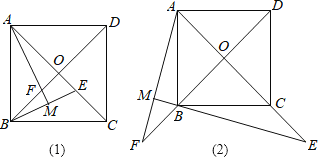
(1)猜想:如图(1)线段OE与线段OF的数量关系为 ;
(2)拓展:如图(2),若点E在AC的延长线上,AM⊥BE于点M,AM、DB的延长线相交于点F,其他条件不变,(1)的结论还成立吗?如果成立,请仅就图(2)给出证明;如果不成立,请说明理由.
【答案】(1)![]() ;(2)成立.理由见解析.
;(2)成立.理由见解析.
【解析】
(1)根据正方形的性质对角线垂直且平分,得到OB=OA,又因为AM⊥BE,所以∠MEA+∠MAE=90°=∠AFO+∠MAE,从而求证出Rt△BOE≌Rt△AOF,得到OE=OF.
(2)根据第一步得到的结果以及正方形的性质得到OB=OA,再根据已知条件求证出Rt△BOE≌Rt△AOF,得到OE=OF.
解:(1)正方形ABCD的对角线AC、BD相交于点O,AM⊥BE,
∴∠AOB=∠BOE=∠AMB=90°,
∵∠AFO=∠BFM(对顶角相等),
∴∠OAF=∠OBE(等角的余角相等),
又OA=OB(正方形的对角线互相垂直平分且相等),
∴△BOE≌△AOF(ASA),
∴OE=OF.
故答案为:OE=OF;
(2)成立.理由如下:
证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]()
又∵![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]()
∴![]() ∴
∴![]() ,
,
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市某中学开展以“三创一办”为中心,以“校园文明”为主题的手抄报比赛.同学们积极参与,参赛同学每人交了一份得意作品,所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如下两幅统计图.请你根据图中所给信息解答下列问题:
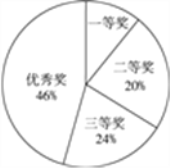

(1)一等奖所占的百分比是__________.
(2)在此次比赛中,一共收到多少份参赛作品?请将条形统计图补充完整.
(3)各奖项获奖学生分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某施工小组乘-辆汽车在东西走向的公路上进行建设,约定向东走为正,某大从![]() 地出发到收工时的行走记录如下(单位:
地出发到收工时的行走记录如下(单位: ![]() );
);![]() ,
,![]() ,求:
,求:
(1)问收工时施工小组是否回到![]() 地,如果回到
地,如果回到![]() 地,请说明理由;如果没有回到
地,请说明理由;如果没有回到![]() 地,请说明检修小组最后的位置:
地,请说明检修小组最后的位置:
(2)距离![]() 地最远的是哪一次?距离多远?
地最远的是哪一次?距离多远?
(3)若汽车每千米耗油![]() 升,开工时储油
升,开工时储油![]() 升,到收工时,中途是否需要加油,若加油最少加多少升?若不需要加油,到收工时,还剩多少升汽油? (假定汽车可以开到油量为
升,到收工时,中途是否需要加油,若加油最少加多少升?若不需要加油,到收工时,还剩多少升汽油? (假定汽车可以开到油量为![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=![]() AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
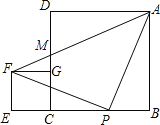
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(1)![]()
(2)计算![]() ,嘉嘉同学的计算过程如下:
,嘉嘉同学的计算过程如下:
原式![]()
请你判断嘉嘉的计算过程是否正确,若不正确,请写出正确的计算过程.
(3)定义一种运算:观察下列各式:![]() ,
,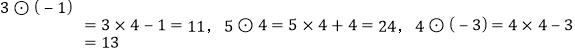 .
.
①请你想一想:![]() .
.
②若![]() ,那么
,那么![]()
![]() (
(![]() 填或
填或![]() )
)
③先化简,在求值:![]() 其中
其中![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米).
表示立方米).
每月用水量 | 单价 |
不超过 | 2元/ |
超出 | 4元/ |
超出 | 8元/ |
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水![]() ,则应收水费_________.元
,则应收水费_________.元
(2)若该户居民3月份用水![]() (其中
(其中![]() ),则应收水费多少元(用含a的代数式表示,并简化).
),则应收水费多少元(用含a的代数式表示,并简化).
(3)若该户居民4,5两个月共用水![]() (5月份用水量超过了4月份),设4月份,用水
(5月份用水量超过了4月份),设4月份,用水![]() ,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com