
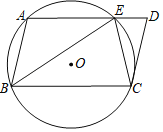
【题目】如图,在ABCD中,过A、B、C三点的⊙O交AD于点E,连接BE、CE,BE=BC.
(1)求证:△BEC∽△CED;
(2)若BC=10,DE=3.6,求⊙O的半径.
【答案】(1)见解析; (2)![]()
【解析】
(1)证明两个等腰三角形相似,证明一个底角对应相等即可;
(2)利用直径构造直角三角形,从而涉及到半径(直径),再利用垂径定理即可解决问题.
(1)证明:∵BE=BC,
∴∠BEC=∠BCE
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠BCE=∠DEC,∠A+∠D=180°.
∴∠BEC=∠DEC
∵四边形ABCD内接于⊙O,
∴∠A+∠BCE=180°.
∴∠BCE=∠D
∴△BEC∽△CED
即得证.
(2)过点O作OF⊥CE,垂足为F,连接OC,如下图.

∴CF=![]() CE,
CE,
∴直线OF垂直平分CE,
∵BE=BC,
∴直线OF经过点B,
∵△BEC∽△CED,又由(1)可知CE=CD,
∴![]() ,
,
∵BC=10,DE=3.6,
∴CE=CD=6
∴CF=![]() CE=3,
CE=3,
设⊙O的半径为r,
可得BF=![]() ,OF=
,OF=![]() ﹣r,
﹣r,
在Rt△OCF中,OF2+CF2=OC2,
∴(![]() ﹣r)2+9=r2
﹣r)2+9=r2
∴r=![]() ,
,
即圆的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 | 单价(元) | 数量(个) | 金额(元) |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是

A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形。如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
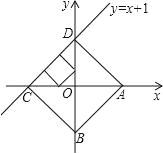
(2)若某函数是反比例函数![]() (k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标_____,写出符合题意的其中一条抛物线解析式_____,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?_____.(本小题只需直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣m)2+2(x﹣m)(m为常数)
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)当m取什么值时,该函数的图象关于y轴对称?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:![]() 、
、![]() 都是关于
都是关于![]() 的多项式,
的多项式,![]() ,
,![]() ,其中多项式
,其中多项式![]() 有一项被“□”遮挡住了.
有一项被“□”遮挡住了.
(1)当![]() 时,
时,![]() ,请求出多项式
,请求出多项式![]() 被“□”遮挡的这一项的系数;
被“□”遮挡的这一项的系数;
(2)若![]() 是单项式,请直接写出多项式
是单项式,请直接写出多项式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
, ![]() ,
,![]() .点
.点![]() 是斜边AB上一个动点.过点
是斜边AB上一个动点.过点![]() 作
作![]() , 垂足为
, 垂足为![]() , 交边
, 交边![]() (或边
(或边![]() ) 于点
) 于点![]() , 设
, 设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数图象大致为( )
之间的函数图象大致为( )
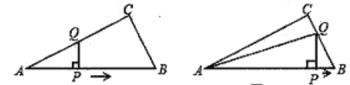
A. 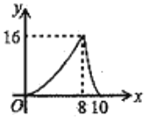 B.
B. 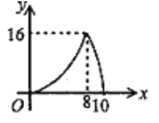
C. 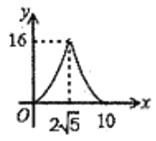 D.
D.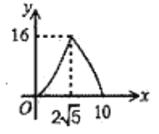
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,边长为1,∠A=60,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去,…,则四边形A2019B2019C2019D2019的面积是_____.
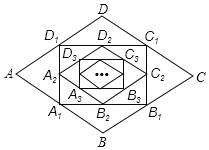
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC≤BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、点F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.
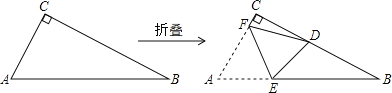
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com