
【题目】已知直线AC经过点(1,5)和(-1,1)与直线BC :y = -2x -1相交于点C 。

(1)求直线AC的解析式.
(2)求直AC与y轴交点A的坐标及直线BC与y轴交点B的坐标.
(3)求两直线交点C的坐标.
(4)求△ABC的面积.
【答案】(1)y=2x+3,(2)A(0.3)B(0,-1)(3)C(-1,1)(4)2.
【解析】
(1)根据待定系数法即可求出直线AC的解析式;
(2)令直线AC的解析式x=0,即可求解出A点坐标,令直线BC解析式x=0,即可求出B点坐标;
(3)联立两函数,解二元一次方程组即可求出C点坐标;
(4)根据三角形的面积公式即可求解.
(1)设AC的直线解析式为y=kx+b,
把(1,5)和(-1,1)代入得![]()
解得![]() ,∴AC的直线解析式为y=2x+3,
,∴AC的直线解析式为y=2x+3,
(2)∵AC的直线解析式为y=2x+3,
令x=0,得y=3,∴A(0.3)
∵直线BC解析式为y = -2x -1
令x=0,得y=-1,∴B(0,-1)
(3)联立两函数得![]() 解得
解得![]()
∴C(-1,1)
(4)∵A(0.3),B(0,-1)∴AB=4,
∵C(-1,1)
∴△ABC的面积为![]() ×4×1=2.
×4×1=2.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,![]() ,
,![]() ,
,![]() ,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿AB向B点运动,设E点的运动时间为t秒,连接DE,当以B、D、E为顶点的三角形与△ABC相似时,t的值为( )
,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿AB向B点运动,设E点的运动时间为t秒,连接DE,当以B、D、E为顶点的三角形与△ABC相似时,t的值为( )
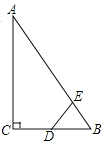
A.2或3.5B.2或3.2C.2或3.4D.3.2或3.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形ABCD在平面直角坐标系中,A、B(点A在点B的左侧)两点的横坐标是方程![]() 的两个根,点D在y轴上其中
的两个根,点D在y轴上其中![]() .
.

(1)求平行四边形ABCD的面积;
(2)若P是第一象限位于直线BD上方的一点,过P作![]() 于E,过E作
于E,过E作![]() 轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是
轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是![]() ;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求
;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求![]() 的最小值,此时y轴上有一个动点G,当
的最小值,此时y轴上有一个动点G,当![]() 最大时,求G点坐标;
最大时,求G点坐标;
(3)在(2)的情况下,将△AOD绕O点逆时针旋转60°后得到![]() 如图2,将线段
如图2,将线段![]() 沿着x轴平移,记平移过程中的线段
沿着x轴平移,记平移过程中的线段![]() 为
为![]() ,在平面直角坐标系中是否存在点S,使得以点
,在平面直角坐标系中是否存在点S,使得以点![]() ,
,![]() ,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+xy+2y-1,B=2x2-xy
(1)若(x+1)2+|y-2|=0,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车一天下午某时间段以广场为出发点,在东西方向的大道上营运,规定向东为正,向西为负,单次行车里程依先后顺序记录如下:(单位:![]() )+9,-3,-5,+4,-8,+7,-2,-5,+8,-4
)+9,-3,-5,+4,-8,+7,-2,-5,+8,-4
(1)该出租车司机将最后一名乘客送到目的地后,出租车在广场的什么方向?距广场多远?
(2)若每千米耗油0.08升,该出租车这个时间段共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
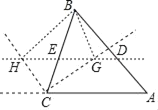
A. 若BG∥CH,则四边形BHCG为矩形
B. 若BE=CE时,四边形BHCG为矩形
C. 若HE=CE,则四边形BHCG为平行四边形
D. 若CH=3,CG=4,则CE=2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次为地震灾区的捐款活动中,某校随机调查了50名学生的捐款情况,统计如表:
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 10 | 12 | 3 |
(1)这50名学生捐款金额的众数和中位数分别为多少元?
(2)如果把这50名学生的捐款情况绘制成扇形统计图,则捐款金额为15元的人数所对应的扇形圆心角为多少度?
(3)若该校共有1200名学生,估计该校的捐款总数大约是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
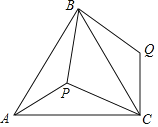
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE∶CD=5∶24
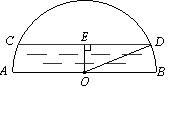
(1)求CD的长;
(2)现汛期来临,水面要以每小时4 m的速度上升,则经过多长时间桥洞会刚刚被灌满?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com