
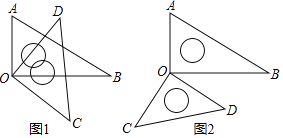
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图1,若∠BOD=25°,则∠AOC= °;若∠AOC=125°,则∠BOD= °;
(2)如图2,若∠BOD=50°,则∠AOC= °;若∠AOC=140°,则∠BOD= °;
(3)猜想∠AOC与∠BOD的大小关系: ;并结合图(1)说明理由.
【答案】(1)155,55;(2)130,40;(3)∠AOC与∠BOD互补,理由见解析.
【解析】
(1)由于是两直角三角形板重叠,根据∠AOC=∠AOB+∠COD﹣∠BOD可分别计算出∠AOC、∠BOD的度数;
(2)根据∠AOC=∠AOB+∠COD﹣∠BOD计算可得;
(3)由∠AOD+∠BOD+∠BOD+∠BOC=180![]() 且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补.
且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补.
解:(1)若∠BOD=25![]() ,
,
∵∠AOB=∠COD=90![]() ,
,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90![]() +90
+90![]() ﹣25
﹣25![]() =155
=155![]() ,
,
若∠AOC=125![]() ,
,
则∠BOD=∠AOB+∠COD﹣∠AOC=90![]() +90
+90![]() ﹣125
﹣125![]() =55
=55![]() ;
;
故答案为:155,55.
(2)若∠BOD=50![]() ,
,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90![]() +90
+90![]() ﹣50
﹣50![]() =130
=130![]() ,
,
若∠AOC=140![]() ,
,
则∠BOD=360![]() ﹣∠AOC﹣∠AOB﹣∠COD=40
﹣∠AOC﹣∠AOB﹣∠COD=40![]() ;
;
故答案为:130,40.
(3)∠AOC与∠BOD互补.
∵∠AOD+∠BOD+∠BOD+∠BOC=180![]() ,∠AOD+∠BOD+∠BOC=∠AOC,
,∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180![]() ,
,
即∠AOC与∠BOD互补.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:
① (﹣21)+(﹣13)﹣(﹣25)﹣(+28)
② ﹣22﹣6÷(﹣2)×![]()
③先化简再求值:﹣a2b+(3ab2﹣a2b)﹣2(2ab2﹣a2b),其中 a=﹣1,b=﹣2.
(2)解下列方程
①x=1-(3 x-1)
② ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在![]() 两地分别库存有挖掘机16台和12台,现在运往甲、乙两地支援建设,其中甲地需要15台,乙地需要13台.从
两地分别库存有挖掘机16台和12台,现在运往甲、乙两地支援建设,其中甲地需要15台,乙地需要13台.从![]() 地运一台到甲、乙两地的费用分别是500元和400元;从
地运一台到甲、乙两地的费用分别是500元和400元;从![]() 地运一台到甲、乙两地费用分别是300元和600元,设从
地运一台到甲、乙两地费用分别是300元和600元,设从![]() 地运往甲地
地运往甲地![]() 台挖掘机.
台挖掘机.
(1)请补全下表,并求出运这批挖掘机的总费用是多少?
甲 | 乙 | 总计 | |
|
| ____________台 | 16台 |
| _______________台 | ____________台 | 12台 |
总计 | 15台 | 13台 | 28台 |
(2)当从![]() 地运往甲地5台挖掘机时,运这批挖掘机的总费用是多少?
地运往甲地5台挖掘机时,运这批挖掘机的总费用是多少?
(3)怎样安排运输方案,可使运这批挖掘机的总费用最少,最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长60cm,一根长100cm,将它们的一个端点重合,放在同一条直线上,此时两根木条中点间的距离( )
A.20cmB.80cm
C.160cmD.20cm 或80cm
查看答案和解析>>
科目:初中数学 来源: 题型:
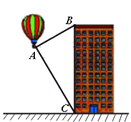
【题目】热气球的探测器显示,从热气球A看一栋高楼顶部B处的仰角为30,看这栋高楼底部C处的俯角为60,若热气球与高楼的水平距离为90 m,则这栋高楼有多高?(结果保留整数,![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)找规律:1,2,4,8……,则第n个数为________.
(2)求和![]() ,观察发现,从第2个加数起每一个加数都是前一个加数的2倍.于是可假设:
,观察发现,从第2个加数起每一个加数都是前一个加数的2倍.于是可假设:![]() ①
①
两边乘以2得:![]() ②
②
②-①得:![]() ,所以:
,所以:![]()
类比做一做,求![]() 的值.
的值.
(3)仿照(2)的做法求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=![]() +bx+c图像的一部分,图像过点A(-3,0),对称轴是直线x=-1,给出四个结论,其中正确结论的个数为( )
+bx+c图像的一部分,图像过点A(-3,0),对称轴是直线x=-1,给出四个结论,其中正确结论的个数为( )
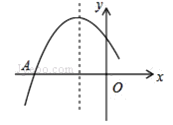
①c>0; ② 2a-b=0; ③![]() <0. ④若点B(-
<0. ④若点B(-![]() ,
,![]() )、C(-
)、C(-![]() ,
,![]() )在图像上,则
)在图像上,则![]() <
<![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
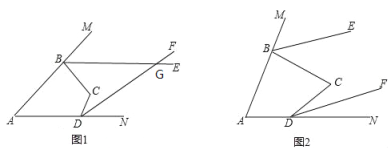
【题目】如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β
(1)如图,若α+β=120°,求∠MBC+∠NDC的度数;
(2)如图,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系式;
(3)如图,若α=β,判断BE、DF的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com