
【题目】已知,如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CG=EG
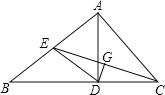
(1)求证:CD=AE;
(2)若AD=BD,CD=2,则求△ABD的面积.
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在锐角三角形ABC中,AB=8,AC=5,BC=6,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,下列结论:①∠CBD=∠EBD,②DE⊥AB,③三角形ADE的周长是7,④![]() ,⑤
,⑤![]() .其中正确的个数有( )
.其中正确的个数有( )
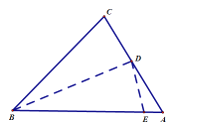
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
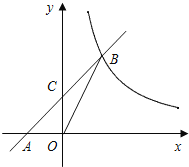
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①若ab=0,则P(a,b)在坐标原点;②在平面直角坐标系中,若A(﹣1,﹣2),且AB平行于x轴,AB=5,则B点的坐标为(4,﹣2);③在平面直角坐标系中点,P(1,2)关于原点对称的点的坐标是(﹣1,﹣2);④若关于x的一元一次不等式组![]() 无解,则a的取值范围是a>1,其中真命题的个数为( )
无解,则a的取值范围是a>1,其中真命题的个数为( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1)![]() 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
![]() 求
求![]() 的值;
的值;
![]() 若CD=2,求BP的长.
若CD=2,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明:小强想证明下面的问题:“有两个角(图中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的
)相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的![]() 和边
和边![]() .
.
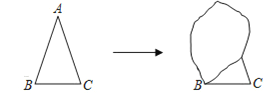
(1)请问:他能够把图恢复成原来的样子吗?若能,请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子.

(2)你能够证明这样的三角形是等腰三角形吗?(至少用两种方法证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
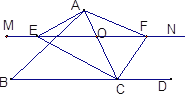
⑴说明:OE=OF
⑵当点O运动到何处时,四边形AECF是矩形,证明你的结论
⑶在⑵的条件下,当⊿ABC满足什么条件时,四边形AECF为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=![]() ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com