
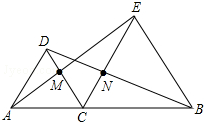
 如图,△DAC和△EBC均是等边三角形,AB、BC分别与CD、CE交于点M、N,有如下结论:
如图,△DAC和△EBC均是等边三角形,AB、BC分别与CD、CE交于点M、N,有如下结论:| A、3个 | B、2个 | C、1个 | D、0个 |
|
|


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
| A、“打开电视机,正在播NBA篮球赛”是必然事件 | ||||
B、“掷一枚硬币正面朝上的概率是
| ||||
| C、一组数据2,3,4,5,5,6的众数和中位数都是5 | ||||
D、甲组数据的方差
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2x2y+3xy2=5x3y |
| B、(-x)3•(-x)2=-x5 |
| C、(-a3)2+(-a2)3=1 |
| D、2x3+x2=3x5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、两个有理数的和一定大于其中任何一个加数 |
| B、零加上一个数仍得这个数 |
| C、两个有理数的差一定小于被减数 |
| D、零减去一个数仍得这个数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com