
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.
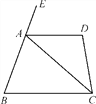
(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
【答案】(1)AD与BC平行;(2)70°.
【解析】试题分析:(1)根据角平分线的定义求出∠BCD,得到∠D+∠BCD=180°,根据平行线的判定即可推理.
(2)根据平行线的性质求出∠DAC,代入∠EAD=180°-∠DAC-∠BAC求出即可.
试题解析:
(1)AD∥BC ,
∵AC平分∠BCD,∠ACB=40°,
∴∠BCD=2∠ACB=80° ,
∵∠D=100°,
∴∠D+∠BCD=180° ,
∴AD∥BC.
(2)∵AD∥BC,∠ACB=40°,
∴∠DAC=∠ACB=40°,
∵∠BAC=70°,
∴∠DAB=∠DAC+∠BAC=40°+70°=110° ,
∴∠EAD=180°-∠DAB=180°-110°=70°.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
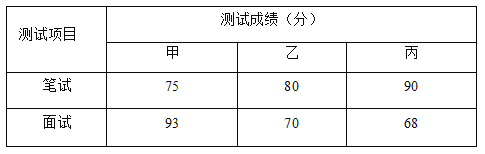
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记作1分.
(1)请算出三人的民主评议得分.
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到0.01)?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按2:1:2的比例确定个人成绩,那么谁将被录用?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数 6, 3, 2, 1, 6中,取三个数相乘,能够得到最大的乘积是_________,再从中取三个数相加,能够得到最小的和是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,AC=BC,AB=4![]() ,D是AB的中点,连结DC,E为DC中点,连接AE,延长AE交BC于F,过点C作CG⊥AF,垂足是G,连接DG,则∠DGA=_______,DG=________
,D是AB的中点,连结DC,E为DC中点,连接AE,延长AE交BC于F,过点C作CG⊥AF,垂足是G,连接DG,则∠DGA=_______,DG=________
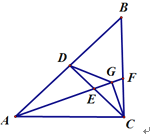
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根弹簧原长10厘米,挂重物后(不超过50克),它的长度会改变,请根据下面表格中的一些数据回答下列问题:
质量(克) | 1 | 2 | 3 | 4 | ……n |
伸长量(厘米) | 0.5 | 1 | 1.5 | 2 | …… |
总长度(厘米) | 10.5 | 11 | 11.5 | 12 | …… |
(1)要想使弹簧伸长5厘米,应挂重物多少克?
(2)当所挂重物为x克时,用代数式表示此时弹簧的总长度.
(3)当x=30克时,求此时弹簧的总长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天生产4500个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋 x个.
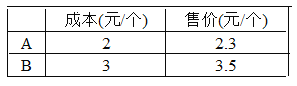
(1)用含x的整式表示每天的生产成本,并进行化简;
(2)用含x的整式表示每天获得的利润,并进行化简(利润=售价-成本);
(3)当x=1500时,求每天的生产成本与每天获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察:从2开始,连续的偶数相加,它们的和的情况如下图:
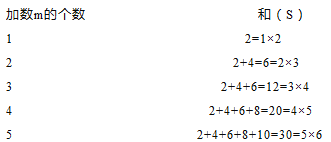
(1)和S与加数的个数m之间的数量关系为S= (用含m 的代数式表示);
(2)按此规律计算(写出必要的演算过程):
(i)2+4+6+┈+300 的值;
(ii)162+164+166+┈+400 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com