
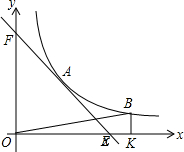
 已知A(m,2)是直线L和双曲线y=
已知A(m,2)是直线L和双曲线y=| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
|
|
| 1 |
| 2 |
 (3)存在.理由如下:
(3)存在.理由如下:| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、春林高级中学为了改善办学条件,2001年暑假对高中部内道长300米的操场投资修建塑胶跑道.请你根据图上所示数据完成下列各题(π取3.14):
23、春林高级中学为了改善办学条件,2001年暑假对高中部内道长300米的操场投资修建塑胶跑道.请你根据图上所示数据完成下列各题(π取3.14):查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com