已知在直角坐标系xOy中,二次函数y=-x2+bx+c的图象经过点A(-2,3)和点B(0,-5).
(1)求这个二次函数的解析式;
(2)将这个函数的图象向右平移,使它再次经过点B,并记此时函数图象的顶点为M.如果点P在x轴的正半轴上,且∠MPO=∠MBO,求∠BPM的正弦值.
【答案】
分析:(1)抛物线的解析式中有两个待定系数,直接将已知的两点坐标代入其中,即可求出待定系数的值,由此得解.
(2)可先求出点A或B关于抛物线对称轴的对称点,据此找出抛物线平移的距离,由此先得出点M的坐标;若∠MBO=∠MPO,那么它们加上一对对顶角后可发现,∠BMP=∠BOP=90°,即△MPB是直角三角形,首先利用勾股定理确定点P的坐标,则BM、PM的长可知,进而可得到∠BPM的正弦值.
解答:解:(1)由题意,得

,
解得
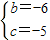
;
∴所求二次函数的解析式为y=-x
2-6x-5.
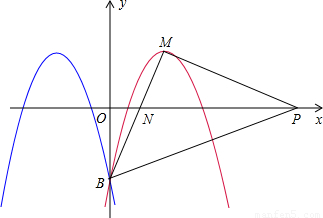
(2)二次函数y=-x
2-6x-5图象的顶点坐标为(-3,4),且经过点(-6,-5);
∴图象向右平移6个单位,平移后的顶点M的坐标为(3,4).
由题意∠MPO=∠MBO,由右图知:∠MNP=∠BNO,可得:
∠MPO+∠MNP=∠MBO+∠BNO,即:∠PMB=∠POB=90°.
已知B(0,-5)、M(3,4),设点P的坐标为(x,0),则:
BM
2=(0-3)
2+(-5-4)
2=90、MP
2=(x-3)
2+16、BP
2=x
2+25;
∴(x-3)
2+16+90=x
2+25,解得 x=15;
∴点P的坐标为(15,0).
∴BM=3
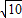
,PB=5
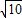
.
∴sin∠BPM=

.
点评:此题主要考查的是函数解析式的确定以及解直角三角形的相关知识;题目的难度不大,最后一题中,准确判断出∠PMB的度数是解答题目的关键所在.

 ,
,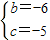 ;
; (2)二次函数y=-x2-6x-5图象的顶点坐标为(-3,4),且经过点(-6,-5);
(2)二次函数y=-x2-6x-5图象的顶点坐标为(-3,4),且经过点(-6,-5);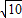 ,PB=5
,PB=5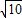 .
. .
.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案 .折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上.
.折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上.