
 如图:在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移到BC,使B(0,b),且a,b满足|2-a|+$\sqrt{6+b}$=0
如图:在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移到BC,使B(0,b),且a,b满足|2-a|+$\sqrt{6+b}$=0分析 (1)根据非负数的性质即可得到结果;
(2)根据勾股定理求得AB的长度,求出直线AB的解析式,然后根据点到直线的距离即可得到结果;
(3)分两种情况:①当点P在点A的右侧如图1,连接PC,延长BC交x轴于E,②当点P在点A的左侧如图2,连接PC,延长DA交PC于F,根据平移的性质和外角的性质即可得到结论.
解答 解:(1)∵a,b满足|2-a|+$\sqrt{6+b}$=0,
∴2-a=0,6+b=0,
∴a=2,b=-6,
∴A(2,0),B(0,-6);
(2)由(1)得A(2,0),B(0,-6),
∴OA=2,OB=6,
∴AB=$\sqrt{A{O}^{2}+O{B}^{2}}$=2$\sqrt{10}$,
∵三角形ABM的面积为16,
∴点M到直线AB的距离为:$\frac{8\sqrt{10}}{5}$,
∴直线AB的解析式为:y=3x-6,
根据点到直线的距离得:$\frac{|3×(-3)-n-6|}{\sqrt{{3}^{2}+(-1)^{2}}}$=$\frac{8\sqrt{10}}{5}$,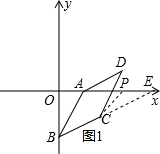
解得:n=1或n=-31;
(3)①当点P在点A的右侧如图1,连接PC,延长BC交x轴于E,
∵AD平移到BC,
∴AD∥BC,
∵∠DAO=150°,
∴∠DAE=30°,
∵∠AEC=30°,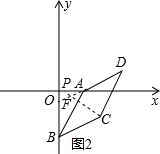
∴∠PCE=∠APC-30°,
∵∠PCB+∠PCE=∠PCB+∠APC-30°=180°,
∴∠PCB+∠APC=210°;
②当点P在点A的左侧如图2,连接PC,延长DA交PC于F,
∵∠DAO=150°,
∴∠PAF=30°,
∵AD∥BC,
∴∠AFC=∠PCB,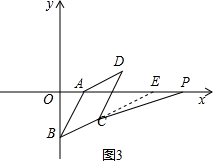
∵∠AFC=∠APC+30°,
∴∠PCB-∠APC=30°;
③当p在直线BC与x轴交点的右侧时,
∵∠DAO=150°,
∴∠DAP=30°,
∴∠OEC=30°,
∴∠ECP=30°-∠APC,
∴∠BCP=180°-∠ECP=150°+∠APC,
∴∠BCP-∠APC=150°.
点评 本题考查了坐标与图形的关系,平移的性质,三角形的面积,勾股定理,点到直线的距离公式,正确的画出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
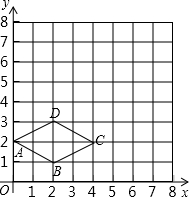 如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.
如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
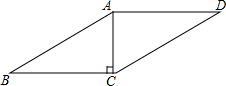 如图,在?ABCD中,过A点作高,垂足刚好为点C,AB=4,AC=2,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AB=4,AC=2,则?ABCD的周长是( )| A. | 8+4$\sqrt{3}$ | B. | 4+2$\sqrt{3}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com