
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,D,E分别为AC,BC上的点,且CE=CD,连接DE,AD,BE,F为线段AD的中点,连接CF.
(1)求证:BE=2CF;
(2)如图2,把△DEC绕点C顺时针旋转α角(0°<α<90°),其他条件不变,试探究线段BE与CF的位置关系,并说明理由;
(3)如图3,把△DEC绕点C顺时针旋转45°,BE,CD交于点G.若∠DCF=30°,求![]() 及
及![]() 的值.
的值.

【答案】(1)证明见解析;
(2)BE⊥CF.证明见解析;
(3)![]() ,
, ![]()
【解析】试题分析:(1)根据已知条件易证△BCE≌△ACD,即可得BE=AD,∠EBC=∠DAC,再由F为线段AD的中点可得CF=AF=DF=![]() AD,即可证得结论;(2)延长CF到H,使HF=CF,连接AH、DH,易得四边形AHDC为平行四边形,根据平行四边形的性质可得AH=CD=CE,∠CAH=180°-∠ACD,再由∠BCE=∠BCA+∠DCE-∠ACD=180°-∠ACD,即可得∠CAH=∠BCE,再判定△CAH≌△BCE,根据全等三角形的性质可得∠ACH=∠CBE,所以∠CBE+∠BCH=∠ACH+∠BCH=90°,即可得结论BE⊥CF ;( 3)设BE,CF相交于点O,则∠GOC=90°,作BC的垂直平分线,交BG于点M,连接CM则BM=CM,∠MBC=∠MCB,所以∠OMC=2∠MBC,再求得∠DCA=45°,∠OMC=30°,设OG=x,则CG=2x,OC=
AD,即可证得结论;(2)延长CF到H,使HF=CF,连接AH、DH,易得四边形AHDC为平行四边形,根据平行四边形的性质可得AH=CD=CE,∠CAH=180°-∠ACD,再由∠BCE=∠BCA+∠DCE-∠ACD=180°-∠ACD,即可得∠CAH=∠BCE,再判定△CAH≌△BCE,根据全等三角形的性质可得∠ACH=∠CBE,所以∠CBE+∠BCH=∠ACH+∠BCH=90°,即可得结论BE⊥CF ;( 3)设BE,CF相交于点O,则∠GOC=90°,作BC的垂直平分线,交BG于点M,连接CM则BM=CM,∠MBC=∠MCB,所以∠OMC=2∠MBC,再求得∠DCA=45°,∠OMC=30°,设OG=x,则CG=2x,OC=![]() x,BM=CM=2
x,BM=CM=2![]() x,OM=
x,OM=![]() OC=3x,MG=3x-x=2x,求得BG=BM+MG=2
OC=3x,MG=3x-x=2x,求得BG=BM+MG=2![]() x+2x,BO=BM+MO=2
x+2x,BO=BM+MO=2![]() x+3x,即可得
x+3x,即可得![]() ,
, ![]() ,过E作BC的垂线,交BC的延长线于N,则Rt△BNE∽Rt△BOC,可得
,过E作BC的垂线,交BC的延长线于N,则Rt△BNE∽Rt△BOC,可得![]() ,设EN=t,则CN=
,设EN=t,则CN=![]() t,CE=t,BN=(
t,CE=t,BN=(![]() +2)t,BC=(
+2)t,BC=(![]() +2)t-t=(
+2)t-t=(![]() +1)t,求得
+1)t,求得![]() 的值,又因AB=BC,CD=CE,即可求得
的值,又因AB=BC,CD=CE,即可求得![]() 的值.
的值.
试题解析:
(1)证明:∵AC=BC,DC=EC,∠ACB=90°
∴△BCE≌△ACD
∴BE=AD,∠EBC=∠DAC
∵F为线段AD的中点
∴CF=AF=DF= ![]() AD
AD
∴BE=2CF
(2)BE⊥CF.证明如下:
证明:如图2,延长CF到H,使HF=CF,连接AH、DH

∵AF=DF,∴四边形AHDC为平行四边形
∴AH=CD=CE,∠CAH=180°-∠ACD
∵∠BCE=∠BCA+∠DCE-∠ACD=180°-∠ACD
∴∠CAH=∠BCE
又∵AC=BC,∴△CAH≌△BCE
∴∠ACH=∠CBE
∴∠CBE+∠BCH=∠ACH+∠BCH=90°
∴BE⊥CF
(3)如图3,设BE,CF相交于点O,

则∠GOC=90°
作BC的垂直平分线,交BG于点M,连接CM
则BM=CM,∠MBC=∠MCB
∴∠OMC=2∠MBC
∵AC⊥DE,∠CDE=45°,∴∠DCA=45°
∵∠DCF=30°
∴∠ACO=∠CBE=15°,∴∠OMC=30°
设OG=x,则CG=2x,OC=![]() x,BM=CM=2
x,BM=CM=2![]() x
x
OM=![]() OC=3x,MG=3x-x=2x
OC=3x,MG=3x-x=2x
∴BG=BM+MG=2![]() x+2x,BO=BM+MO=2
x+2x,BO=BM+MO=2![]() x+3x
x+3x
∴![]() =
= ![]() =
=![]() +1
+1
![]() =
= ![]() =
=![]() +2
+2
过E作BC的垂线,交BC的延长线于N
则Rt△BNE∽Rt△BOC,∴![]() =
= ![]() =
=![]() +2
+2
设EN=t,则CN=t,CE=![]() t,BN=(
t,BN=(![]() +2)t,BC=(
+2)t,BC=(![]() +2)t-t=(
+2)t-t=(![]() +1)t
+1)t
∴![]() =
= ![]() =
= ![]()
∵AB=BC,CD=CE,∴ ![]() =
= ![]()


科目:初中数学 来源: 题型:
【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需( )
A.28mn 元 B.11mn元 C.(7m+4n)元 D.(4m+7n)元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:

(1)根据上图中提供的数据列出如下统计表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BD为∠ABC的平分线.
(1)如图1,∠C=2∠DBC,∠A=60°,求证:△ABC为等边三角形;
(2)如图2,若∠A=2∠C,BC=8,AB=4.8,求AD的长度;
(3)如图3,若∠ABC=2∠ACB,∠ACB的平分线OC与BD相交于点O,且OC=AB,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
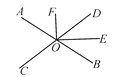
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.

(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百货商场试销一批新款衬衫,一周内销售情况如表所示,商场经理想要了解哪种型号最畅销,那么他最关注的统计量是( )
型号(厘米) | 38 | 39 | 40 | 41 | 42 | 43 |
数量(件) | 23 | 31 | 35 | 48 | 29 | 8 |
A. 平均数 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数y=﹣ ![]() x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( ) 
A.4
B.![]()
C.2π
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com