

|
| ON |
| OA |
| 2 |
| 6 |
| 1 |
| 3 |
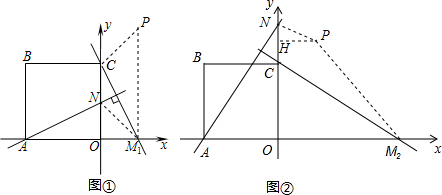 2)①如图①,当CN∥PM时,
2)①如图①,当CN∥PM时,| PH |
| OM |
| NH |
| OC |
| 3 |
| a |
| a-8 |
| 6 |
| 34 |
| 34 |
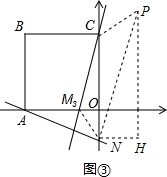 当CM∥PN时,
当CM∥PN时,| PH |
| OC |
| NH |
| OM |
| 8+b |
| 6 |
| 3 |
| b |
| 34 |
| 34 |
| 34 |
| 34 |
| 1 |
| 3 |
| 34 |
| 34 |


科目:初中数学 来源:不详 题型:解答题
 元.又知“为民”出租车公司有小、中、大三种型号货车供出租,本次派出的货车每种型号货车不少于3台,各种型号货车载重量和预计运费如下表所示.
元.又知“为民”出租车公司有小、中、大三种型号货车供出租,本次派出的货车每种型号货车不少于3台,各种型号货车载重量和预计运费如下表所示.| 小 | 中 | 大 | |
| 载重(吨/台) | 12 | 15 | 20 |
| 运费(元/辆) | 1000 | 1200 | 1500 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| ||
| 6 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
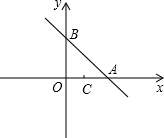 点C(1,0),且把△AOB分成两部分.
点C(1,0),且把△AOB分成两部分.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
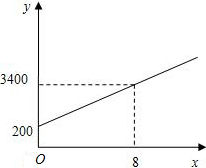
 甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 格不变,而制版费900元按六折收费,且甲乙两厂都规定一次印刷数量至少是500份.
格不变,而制版费900元按六折收费,且甲乙两厂都规定一次印刷数量至少是500份.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,且半圆与y轴的交点D在射线AE的反向延长线上.
,且半圆与y轴的交点D在射线AE的反向延长线上.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
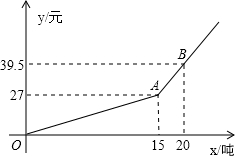 )与用水量x(吨)的函数关系如图所示.
)与用水量x(吨)的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com