
【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
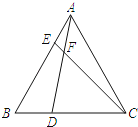
(1)求证:AD=CE;
(2)求∠DFC的度数.
科目:初中数学 来源: 题型:
【题目】某公交车原坐有22人,经过3个站点时上下车情况如下(上车为正,下车为负):(+4,8),(5,6),(3,2),则车上还有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE是中线,AD是角平分线,AF是高,∠B=30°,∠C=80°,BE=3,AF=2,填空:

(1)AB= ;
(2)∠BAD= ;
(3)∠DAF= ;
(4)S△AEC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;
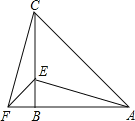
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小芳有两根长度分别为4cm和9cm的木条,他想钉一个三角形木框,桌子上有下列长度的几根木条,她应该选择的木条的长度只能是( )
A. 5cm B. 3cm C. 17cm D. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列已知条件,能惟一画出△ABC的是( )
A. AB=3,BC=4,CA=8 B. ∠A=60°,∠B=45°,AB=4
C. AB=4,BC=3,∠A=30° D. ∠C=90°,AB=6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com