
【题目】如图,在ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M. 
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
【答案】
(1)解:方法一:如图①,
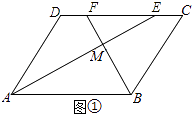
∵在ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
方法二:如图②,延长BC、AE相交于点P,
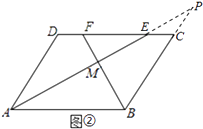
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴AB=BP.
∵BF平分∠ABP,
∴AP⊥BF,
即AE⊥BF
(2)解:方法一:线段DF与CE是相等关系,即DF=CE,
∵在ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.
∴∠DEA=∠DAE.
∴DE=AD.
同理可得,CF=BC.
又∵在ABCD中,AD=BC,
∴DE=CF.
∴DE﹣EF=CF﹣EF.
即DF=CE.
方法二:如图,延长BC、AE设交于点P,延长AD、BF相交于点O,
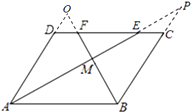
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴BP=AB.
同理可得,AO=AB.
∴AO=BP.
∵在ABCD中,AD=BC,
∴OD=PC.
又∵在ABCD中,DC∥AB,
∴△ODF∽△OAB,△PCE∽△PBA.
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
∴DF=CE.
【解析】(1)因为AE,BF分别是∠DAB,∠ABC的角平分线,那么就有∠MAB= ![]() ∠DAB,∠MBA=
∠DAB,∠MBA= ![]() ∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB. 
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件“∠DAB=∠60°”,(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1 , l2 , l3上,且l1 , l2之间的距离为2,l2 , l3之间的距离为3,则AC的长是( ) 
A.![]()
B.![]()
C.![]()
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
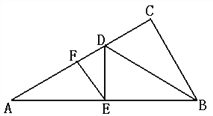
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥AC于F。
(1)求证:△EDF∽△ADE;
(2)猜想:线段DC、DF、DA之间存在什么关系?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
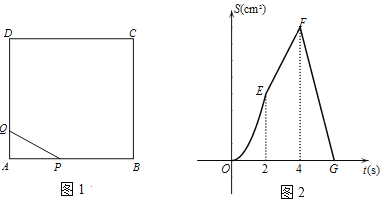
【题目】如图1,四边形![]() 是正方形,动点
是正方形,动点![]() 从点
从点![]() 出发,以
出发,以![]() cm/s的速度沿边
cm/s的速度沿边![]() 、
、![]() 、
、![]() 匀速运动到
匀速运动到![]() 终止;动点
终止;动点![]() 从
从![]() 出发,以
出发,以![]() cm/s的速度沿边
cm/s的速度沿边![]() 匀速运动到
匀速运动到![]() 终止,若
终止,若![]() 、
、![]() 两点同时出发,运动时间为
两点同时出发,运动时间为![]() s,△
s,△![]() 的面积为
的面积为![]() cm2.
cm2. ![]() 与
与![]() 之间函数关系的图像如图
之间函数关系的图像如图![]() 所示.
所示.
(1)求图![]() 中线段
中线段![]() 所表示的函数关系式;
所表示的函数关系式;
(2)当动点![]() 在边
在边![]() 运动的过程中,若以
运动的过程中,若以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 的值;
的值;
(3)是否存在这样的![]() ,使
,使![]() 将正方形
将正方形![]() 的面积恰好分成
的面积恰好分成![]() 的两部分?若存在,求出这样的
的两部分?若存在,求出这样的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积. 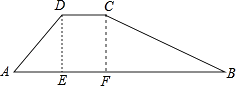
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从![]() 年底的
年底的![]() 万个增长到
万个增长到![]() 年底的
年底的![]() 万个,求该市这两年(从
万个,求该市这两年(从![]() 年底到
年底到![]() 年底)拥有的养老床位数的平均年增长率;
年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共![]() 间,这三类养老专用房间分别为单人间(
间,这三类养老专用房间分别为单人间(![]() 个养老床位),双人间(
个养老床位),双人间(![]() 个养老床位),三人间(
个养老床位),三人间(![]() 个养老床位),因实际需要,单人间房间数在
个养老床位),因实际需要,单人间房间数在![]() 至
至![]() 之间(包括
之间(包括![]() 和
和![]() ),且双人间的房间数是单人间的
),且双人间的房间数是单人间的![]() 倍,设规划建造单人间的房间数为
倍,设规划建造单人间的房间数为![]() .
.
①若该养老中心建成后可提供养老床位![]() 个,求
个,求![]() 的值;
的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com