
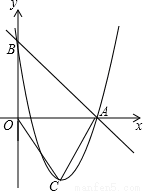
如图,在直角坐标平面内,直线y=-x+5与x轴和y轴分别交于A、B两点,二次函数y=x2+bx+c的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且△ABP的面积为10,求点P的坐标.
(1)y=x2-6x+5;(2)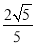 ;(3)P(4,-3).
;(3)P(4,-3).
【解析】
试题分析:(1)根据直线方程求得点A、B的坐标;然后把点A、B的坐标代入二次函数解析式,通过方程组来求系数b、c的值;
(2)如图,过点C作CH⊥x轴交x轴于点H,构建等腰△AOC.则∠OAC=∠OCA,故sin∠OCA=sin∠OAC=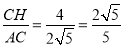 ;
;
(3)如图,过P点作PQ⊥x轴并延长交直线y=-x+5于Q.设点P(m,m2-6m+5),Q(m,-m+5),则PQ=-m+5-(m2-6m+5)=-m2+5m.由S△ABP=S△PQB+S△PQA得到:10=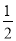 (?m2+5m)×5,则易求m的值.注意点P位于第四象限.
(?m2+5m)×5,则易求m的值.注意点P位于第四象限.
试题解析:(1)由直线y=-x+5得点B(0,5),A(5,0),
将A、B两点的坐标代入y=x2+bx+c,得
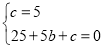 ,
,
解得  ,
,
∴抛物线的解析式为y=x2-6x+5;
(2)如图,过点C作CH⊥x轴交x轴于点H.
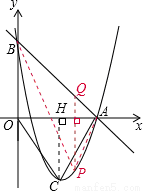
由(1)知,抛物线的解析式为:y=x2-6x+5,则配方 得y=(x-3)2-4,
∴点C(3,-4),
∴CH=4,AH=2,AC=2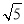
∴OC=5.
∵OA=5,
∴OA=OC,
∴∠OAC=∠OCA,
∴sin∠OCA=sin∠OAC=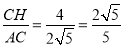
(3)如图,过P点作PQ⊥x轴并延长交直线y=-x+5于Q.
设点P(m,m2-6m+5),Q(m,-m+5),则PQ=-m+5-(m2-6m+5)=-m2+5m.
∵S△ABP=S△PQB+S△PQA=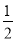 PQ•OA,
PQ•OA,
∴10=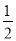 (?m2+5m)×5,
(?m2+5m)×5,
∴m1=1,m2=4,
∴P(1,0)(舍去),P(4,-3).
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年上海市浦东新区中考二模数学试卷(解析版) 题型:选择题
已知抛物线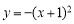 上的两点
上的两点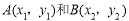 ,如果
,如果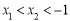 ,那么下列结论一定成立的是
,那么下列结论一定成立的是
(A)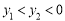 (B)
(B)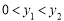 (C)
(C)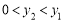 (D)
(D)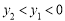 .
.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市毕业生学业模拟考试数学试卷(解析版) 题型:选择题
已知一组数据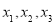 的平均数和方差分别为6和2,则数据
的平均数和方差分别为6和2,则数据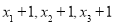 的平均数和方差分别是( )
的平均数和方差分别是( )
(A)6和2 (B)6和3 (C)7和2 (D)7和3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市普陀区中考二模数学试卷(解析版) 题型:选择题
一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的概率为( )
A. 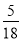 B.
B.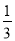 C.
C.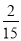 D.
D.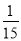
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com