Question

8．如图1，抛物线 y=-$\frac{3}{4}$x²-$\frac{3}{2}$x+6与x轴交于A、B两点（点A在B 的左侧），交y轴交于点C，点D是线段AC的中点，直线BD与抛物线 y=-$\frac{3}{4}$x²-$\frac{3}{2}$x+6交于另一点E，交y轴交于点F．
（1）求直线BE的解析式；
（2）如图2，点P是直线BE上方抛物线上一动点，连接PD、PF，当△PDF的面积最大时，在线段BE上找一点G（不与E、B重合），使得PG-$\frac{3}{5}$GE的值最小，求出点G的坐标及PG-$\frac{3}{5}$GE的最小值；
（3）如图3，将△OBF绕点B顺时针旋转α度（0°＜α＜180°），记旋转过程中的△OBF为△O₁BF₁，直线O₁F₁与x轴交于点M，与直线BE交于点N．在△OBF旋转过程中，是否存在一个合适的位置，使得△MNB是一个等腰三角形？若存在，请直接写出所有符合条件的点N的坐标；若不存在，请说明理由．

Answer 1

分析 （1）先确定出点的坐标，再用待定系数法求出直线解析式；
（2）先判断出取△PDF的面积最大时点P的坐标，然后根据函数解析式依次确定出EK，KM，再判断出△EGN∽△EMK，最后用PG-$\frac{3}{5}$GE的值最小判断出P，M重合，即可．
（3）分三种情况用勾股定理，相似三角形得出的比例式，三角函数计算即可．

解答 解：（1）由 y=-$\frac{3}{4}$x²-$\frac{3}{2}$x+6得：A（-4，0 ），B（2，0），C（0，6）
∵D是线段AC的中点，
∴D（-2，3）
设直线BE的解析式为y=kx+b，代入D（-2，3）、B（2，0）得：
3=-2k+b，0=2k+b，
∴k=-$\frac{3}{4}$，b=$\frac{3}{2}$
∴直线BE的解析式为y=-$\frac{3}{4}$x+$\frac{3}{2}$
（2）如图1，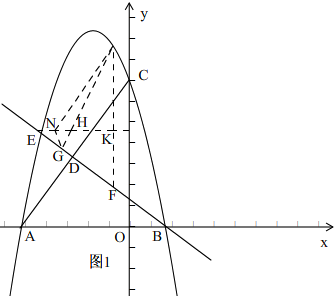

过P作BE的平行线，
故此平行线的解析式为y=-$\frac{3}{4}$x+m，联立y=-$\frac{3}{4}$x²-$\frac{3}{2}$x+6得：
-$\frac{3}{4}$x+b=-$\frac{3}{4}$x²-$\frac{3}{2}$x+6，
∴3x²+3x+4m-24=0，
∴△=3²-4×3（4m-24）=0，
∴m=$\frac{99}{16}$，
∴3x²+3x+4×$\frac{99}{16}$-24=0，
∴4x²+4x+1=0，
∴x₁=x₂=-$\frac{1}{2}$，
∴y=-$\frac{3}{4}$x+m=-$\frac{3}{4}$×（-$\frac{1}{2}$）+$\frac{99}{16}$=$\frac{105}{16}$，
∴P（-$\frac{1}{2}$，$\frac{105}{16}$）
过P作PM⊥x轴，交BE于点M；过E作EK⊥y轴，交PM于点K；在BE上取点G，过G作GN⊥EK于点N．
由 y=-$\frac{3}{4}$x²-$\frac{3}{2}$x+6和y=-$\frac{3}{4}$x+$\frac{3}{2}$得E（-3，$\frac{15}{4}$）
∵P、M的横坐标都是-$\frac{1}{2}$，
∴M（-$\frac{1}{2}$，$\frac{15}{8}$），K（-$\frac{1}{2}$，$\frac{15}{4}$），
∴EK=$\frac{5}{2}$，KM=$\frac{15}{8}$，
∴EM=$\sqrt{E{K^2}+K{M^2}}$=$\frac{25}{8}$，
∴KM：EM=$\frac{15}{8}$：$\frac{25}{8}$，
∴KM=$\frac{3}{5}$EM
∵GN∥KM，
∴△EGN∽△EMK，
∴GN=$\frac{3}{5}$EG，
∴PG-$\frac{3}{5}$GE=PG-GN≥PG-GH=PH≥PK
∴当G与M 重合时PG-$\frac{3}{5}$GE的值最小为PK=PM-KM=$\frac{105}{16}$-$\frac{15}{8}$-$\frac{15}{8}$=$\frac{45}{16}$
∴G点坐标为（-$\frac{1}{2}$，$\frac{15}{8}$），PG-$\frac{3}{5}$GE的值最小为$\frac{45}{16}$
（3）当BM=BN时，有两种情况：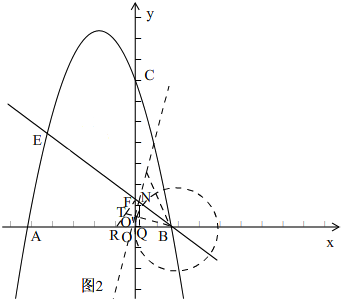

①如图2，在AB上取一点R，使BR=BF，
∵OB=2，OF=$\frac{3}{2}$，
∴BF=$\frac{5}{2}$，
∴OR=BR-OB=BF-OB=$\frac{1}{2}$，
∴RF=$\sqrt{O{R^2}+O{F^2}}$=$\frac{{\sqrt{10}}}{2}$，
∵BF=BR，
∴RT=$\frac{{\sqrt{10}}}{4}$，
∴BT=$\sqrt{B{R^2}-R{T^2}}$=$\frac{{3\sqrt{10}}}{4}$．
∵BM=BN，BF=BR，
∴BM：BF=BN：BR，又∠FBR公共，
∴△BNM∽△BFR，
∴BO'：BT=NM：FR
∴NM=$\frac{4}{3}$，
∴NO'=$\frac{2}{3}$，
∴BN=$\sqrt{{{（{\frac{2}{3}}）}^2}+{2^2}}$=$\frac{{2\sqrt{10}}}{3}$
∵FO∥NQ，
∴BN：BF=NQ：FO，
∴$\frac{{2\sqrt{10}}}{3}$：$\frac{5}{2}$=NQ：$\frac{3}{2}$，
∴NQ=$\frac{{2\sqrt{10}}}{5}$，
∴BQ=$\sqrt{B{N^2}-N{Q^2}}$=$\frac{{8\sqrt{10}}}{15}$，
∴OQ=OB-QB=2-$\frac{{8\sqrt{10}}}{15}$，
∴N点坐标为（2-$\frac{{8\sqrt{10}}}{15}$，$\frac{{2\sqrt{10}}}{5}$）

②如图3，过N作NP⊥x轴．则△NPB∽△FOB，
∴NP：PB=FO：OB=$\frac{3}{2}$：2=$\frac{3}{4}$，
∴设NP=3x，PB=4x，
∴NB=5x，
∴BM=5x，
∴tan∠NMP=NP：PM=3x：（4x+5x）=1：3，
又tan∠O'MB=O'B：O'M，
∴2：O'M=1：3，
∴O'M=6，
∴BM=2$\sqrt{10}$，
∴BN=2$\sqrt{10}$，
由△NPB∽△FOB得NP：FO=BN：FB，
∴NP：$\frac{3}{2}$=2$\sqrt{10}$：$\frac{5}{2}$，
∴NP=$\frac{{6\sqrt{10}}}{5}$，
∴PB=$\frac{{8\sqrt{10}}}{5}$，
∴PO=$\frac{{8\sqrt{10}}}{5}$-2，
∴N点坐标为（2-$\frac{{8\sqrt{10}}}{5}$，$\frac{{6\sqrt{10}}}{5}$）
当MN=MB时，如图4，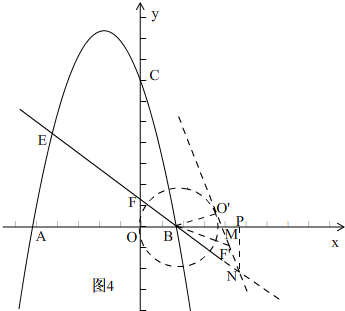

则∠MNB=∠MBN=∠FBO，
∴tan∠MNB=tan∠FBO，
∴O'B：O'N=FO：OB，
∴2：O'N=$\frac{3}{2}$：2，
∴O'N=$\frac{8}{3}$，
∴BN=$\frac{10}{3}$，
同理：sin∠PBN=sin∠FBO，
∴PN：BN=FO：FB，
∴NP=2，
∴BP=$\frac{8}{3}$，
∴OP=$\frac{14}{3}$
∴N 的坐标为（$\frac{14}{3}$，-2）
当NM=NB时，如图5，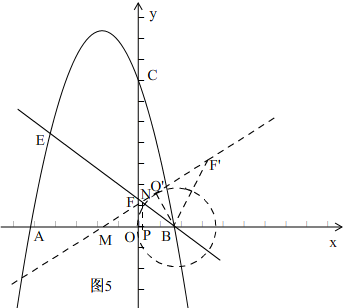

∠NMB=∠NBM，
∴sin∠NMB=sin∠NBM，
∴O'B：MB=OF：FB，
∴2：MB=$\frac{3}{2}$：$\frac{5}{2}$，
∴MB=$\frac{10}{3}$，
过N作NP⊥x轴，则BP=$\frac{1}{2}$MB=$\frac{5}{3}$，
∴NP=$\frac{5}{4}$，
∴N 点坐标为（$\frac{1}{3}$，$\frac{5}{4}$）．

点评 此题是二次函数综合题，主要考查了待定系数法，一元二次方程的根的判别式，勾股定理，相似三角形的性质和判定，锐角三角函数，解本题的关键相似三角形的判定．是一道难度比较大，计算量也较大的压轴题．