
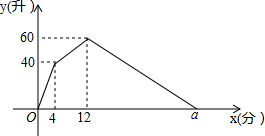
 某容器装有两个相同的注水管和一个出水管,注水管的注水速度和出水管的出水速度均为定值,从某一时刻开始,打开两个注水管向容器内注水4分钟,然后关闭一个注水管,打开出水管.出水管出水8分钟,关闭另一个注水管,容器内的水放完时关闭出水管.容器内的水量y(升)与时间x(分)之间的函数图象如图所示.
某容器装有两个相同的注水管和一个出水管,注水管的注水速度和出水管的出水速度均为定值,从某一时刻开始,打开两个注水管向容器内注水4分钟,然后关闭一个注水管,打开出水管.出水管出水8分钟,关闭另一个注水管,容器内的水放完时关闭出水管.容器内的水量y(升)与时间x(分)之间的函数图象如图所示.分析 (1)设注水管注水量为xL/min,出水管出水量为yL/min,根据:两个注水管4分钟向容器内注水40L,8min一个注水管、一个出水管容器内有水60L,列出方程组,解方程组可得;
(2)待定系数法求解即可;
(3)根据将容器内水量60L÷出水管的出水速度=放完水所需时间,再加12min可得a的值.
解答 解:(1)设注水管注水量为xL/min,出水管出水量为yL/min,
根据题意,得:$\left\{\begin{array}{l}{2×4x=40}\\{40+8x-8y=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=5}\\{y=2.5}\end{array}\right.$,
答:注水管每分钟的注水量为5L,出水管每分钟的出水量2.5L;
(2)设y=kx+b,将点(4,40)、(12,60)代入,
得:$\left\{\begin{array}{l}{4k+b=40}\\{12k+b=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2.5}\\{b=30}\end{array}\right.$,
∴当4≤x≤12时,y与x之间的函数关系式为:y=2.5x+30;
(3)a=$\frac{60}{2.5}$+12=36,
即a=36.
点评 本题考查利用函数的图象解决实际问题和用待定系数法求一次函数的解析式,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
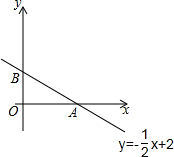 在平面直角坐标系中,已知直线l:y=-$\frac{1}{2}$x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
在平面直角坐标系中,已知直线l:y=-$\frac{1}{2}$x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com