
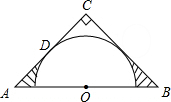
 如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )| A. | 1-$\frac{1}{4}$π | B. | $\frac{1}{2}$-$\frac{π}{8}$ | C. | 2-$\frac{3π}{4}$ | D. | 2-$\frac{1}{4}$π |
分析 根据切线,可得∠ADO=90°,根据AB的长,求出AO的长度;解直角三角形,求出半径OD的长度;根据阴影部分的面积=2×(三角形的面积减扇形的面积),计算即可.
解答 解:如右图,连接OD,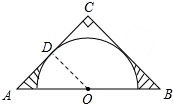
∵AC与⊙O相切,
∴∠ADO=90°,
∵∠C=90°,CA=CB,
∴∠A=∠B=45°,
∴∠AOD=45°,
∵O是AB的中点,AB=2,
∴OA=$\sqrt{2}$,
∴OD=cos45°•OA=$\frac{\sqrt{2}}{2}$,
∴S阴影=2($\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$-$\frac{45π×\frac{1}{2}}{360}$)=$\frac{1}{2}$-$\frac{π}{8}$.
故选B.
点评 本题是切线的性质、等腰三角形的性质、解直角三角形、三角形的面积、扇形的面积的综合应用,根据已知条件求出圆的半径是解决此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
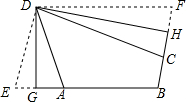 定义:有三个内角相等的四边形叫三等角四边形.
定义:有三个内角相等的四边形叫三等角四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
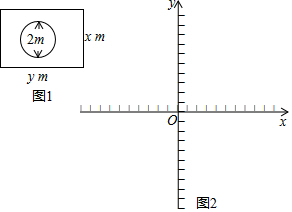 2016年11月28日,神州十一号返回舱成功着陆.假如返回舱着陆后A地为一个直径为2m的圆形,工作人员用警戒带在其外围至少1米外圈成一个面积为80m2的长方形,其俯视如图1所示.设长方形的长为ym,宽为xm.
2016年11月28日,神州十一号返回舱成功着陆.假如返回舱着陆后A地为一个直径为2m的圆形,工作人员用警戒带在其外围至少1米外圈成一个面积为80m2的长方形,其俯视如图1所示.设长方形的长为ym,宽为xm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 计算“$\frac{1}{2}$-1$\frac{3}{4}$”的按键顺序是 | |
| B. | 计算“3×105-28”的按键顺序是 | |
| C. | “已知SinA=0.3,求锐角A”的按键顺序是 | |
| D. | 计算“($\frac{1}{2}$)5”的按键顺序是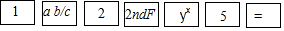 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 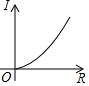 | B. | 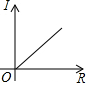 | C. | 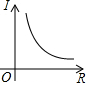 | D. | 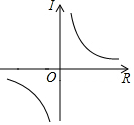 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2m}{{3}^{n}}$ | B. | $\frac{{2}^{m}}{3n}$ | C. | $\frac{2m}{{n}^{3}}$ | D. | $\frac{{m}^{2}}{3n}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com