
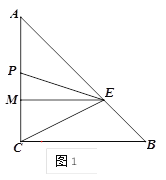
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BC=6ЃЌMЕудкБпACЩЯЃЌЧвCM=2ЃЌЙ§MЕузїACЕФДЙЯпНЛABБпгкEЕуЃЌЖЏЕуPДгЕуAГіЗЂбиACБпЯђMЕудЫЖЏЃЌЫйЖШЮЊ1ИіЕЅЮЛ/УыЃЌЕБЖЏЕуPЕНДяMЕуЪБЃЌдЫЖЏЭЃжЙ.СЌНгEPЁЂECЃЌЩшдЫЖЏЪБМфЮЊtЃЎдкДЫЙ§ГЬжа:
ЃЈ1ЃЉЕБt=1ЪБЃЌЧѓEPЕФГЄЖШЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЁїEPCЪЧЕШбќШ§НЧаЮЃП
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуNЪЧЯпЖЮMEЩЯвЛЕуЃЌЧвMN=3ЃЌЕуQЪЧЯпЖЮAEЩЯвЛЖЏЕуЃЌСЌНгPQЁЂPNЁЂNQЕУЕНЁїPQNЃЌЧыжБНгаДГіЁїPQNжмГЄЕФзюаЁжЕ.

ЁОД№АИЁПЃЈ1ЃЉ5ЃЛЃЈ2ЃЉЕБt=1Лђ2ЛђЃЈ6-2![]() ЃЉЪБЃЌЁїPECЪЧЕШбќШ§НЧаЮЃЛЃЈ3ЃЉЁїPQNжмГЄЕФзюаЁжЕЪЧ
ЃЉЪБЃЌЁїPECЪЧЕШбќШ§НЧаЮЃЛЃЈ3ЃЉЁїPQNжмГЄЕФзюаЁжЕЪЧ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦНааЯпЕФаджЪСаГіБШР§ЪНЃЌЧѓГіEPЃЛ
ЃЈ2ЃЉЗжEP=ECЁЂPC=PEЁЂCP=CEШ§жжЧщПіЃЌИљОнЕШбќШ§НЧаЮЕФИХФюЁЂЙДЙЩЖЈРэМЦЫуМДПЩЃЛ
ЃЈ3ЃЉзїЕуNЙигкACЕФЖдГЦЕуNЁфЃЌЙигкABЕФЖдГЦЕуNЁфЁфЃЌСЌНгNЁфNЁфЁфНЛACгкPЃЌНЛABгкQЃЌСЌНгNЁфЁфEЃЌИљОнЙДЙЩЖЈРэЧѓГіNЁфNЁфЁфЃЌЕУЕНД№АИЃЎ
НтЃКЃЈ1ЃЉЁпЁЯACB=90ЁуЃЌEMЁЭACЃЌ
ЁрEMЁЮBCЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрME=4ЃЌ
ЕБt=1УыЪБЃЌAP=1ЃЌ
дђPM=3ЃЌ
ЁрEP=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБEP=ECЪБЃЌPM=MCЃЌ
Ёр4-t=2ЃЌ
НтЕУЃЌt=2ЃЌ
ЕБPC=PEЪБЃЌЃЈ4-tЃЉ2+42=ЃЈ6-tЃЉ2ЃЌ
НтЕУЃЌt=1ЃЌ
ЕБCP=CEЪБЃЌ22+42=ЃЈ6-tЃЉ2ЃЌ
НтЕУЃЌt1=6+![]() ЃЈЩсШЅЃЉЃЌt2=6-
ЃЈЩсШЅЃЉЃЌt2=6-![]() ЃЌ
ЃЌ
ЕБt=1Лђ2ЛђЃЈ6-2![]() ЃЉЪБЃЌЁїPECЪЧЕШбќШ§НЧаЮЃЛ
ЃЉЪБЃЌЁїPECЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ3ЃЉзїЕуNЙигкACЕФЖдГЦЕуNЁфЃЌЙигкABЕФЖдГЦЕуNЁфЁфЃЌСЌНгNЁфNЁфЁфНЛACгкPЃЌНЛABгкQЃЌСЌНгNЁфЁфEЃЌдђЁїPQNМДЮЊжмГЄзюаЁЕФШ§НЧаЮЃЛ

гЩЬтвтЕУЃЌNЁфE=7ЃЌNЁфЁфE=NE=1ЃЌ
ЁпMEЁЮBCЃЌ
ЁрЁЯAEN=ЁЯB=45ЁуЃЌ
ЁрЁЯNЁфЁфEN=90ЁуЃЌ
ЁрNЁфNЁфЁф=![]() ЃЌ
ЃЌ
дђЁїPQNжмГЄЕФзюаЁжЕЪЧ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌжБЯпaОЙ§е§ЗНаЮABCDЕФЖЅЕуAЃЌЗжБ№Й§е§ЗНаЮЕФЖЅЕуBЁЂDзїBFЁЭaгкЕуFЃЌDEЁЭaгкЕуEЃЌШєDE=8ЃЌBF=5ЃЌдђEFЕФГЄЮЊ__ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧвЛИіДѓГЄЗНаЮМєШЅвЛИіаЁГЄЗНаЮКѓаЮГЩЕФЭМаЮЃЌвбжЊЖЏЕуPвд2cm/sЕФЫйЖШбиЭМаЮБпПђАДBЃCЃDЃEЃFЃAЕФТЗОЖвЦЖЏЃЌЯргІЕФІЄABPЕФУцЛ§SЃЈcmЃЉгыЪБМфtЃЈsЃЉжЎМфЕФЙиЯЕШчЭМЃЌШєAB=8cmЃЌНтД№ЯТСаЮЪЬтЃК


ЃЈ1ЃЉBCЕФГЄЪЧЖрЩйЃП
ЃЈ2ЃЉЭМЯѓжаЕФaЪЧМИЃП
ЃЈ3ЃЉСљБпаЮЕФУцЛ§ЪЧЖрЩйЃП
ЃЈ4ЃЉЭМЯѓжаЕФbЪЧМИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ.дкЁїABCжаЃЌЁЯB=ЁЯC=50ЁуЃЌDЪЧBCЕФжаЕуЃЌDEЁЭABЃЌ DFЁЭACЃЌдђЁЯBAD=_________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
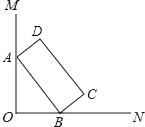
ЁОЬтФПЁПШчЭМЃЌЁЯMON=90ЁуЃЌОиаЮABCDЕФЖЅЕуAЁЂBЗжБ№дкБпOMЃЌONЩЯЃЌЕБBдкБпONЩЯдЫЖЏЪБЃЌAЫцжЎдкOMЩЯдЫЖЏЃЌОиаЮABCDЕФаЮзДБЃГжВЛБфЃЌЦфжаAB=2ЃЌBC=1ЃЌдЫЖЏЙ§ГЬжаЃЌЕуDЕНЕуOЕФзюДѓОрРыЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊОиаЮABCDжаЃЌEЪЧADБпЩЯЕФвЛИіЖЏЕуЃЌЕуFЃЌGЃЌHЗжБ№ЪЧBCЃЌBEЃЌCEЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїBGFЁеЁїFHCЃЛ
ЃЈ2ЃЉЩшAD=aЃЌЕБЫФБпаЮEGFHЪЧе§ЗНаЮЪБЃЌЧѓОиаЮABCDЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЌЕуCЪЧЯпЖЮABЩЯвЛЕуЃЌЕуMЁЂNЗжБ№ЪЧACЁЂBCЕФжаЕуЃЎ
ЂйШєACЃН8cmЃЌCBЃН6cmЃЌЧыЧѓГіЯпЖЮMNЕФГЄЃЛ
ЂкШєЕуCТњзуAC+CBЃНacmЃЌЦфЫќЬѕМўВЛБфЃЌФуФмВТЯыMNЕФГЄЖШТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєCдкЯпЖЮABЕФбгГЄЯпЩЯЃЌЧвТњзуACЉBCЃНbcmЃЌMЁЂNЗжБ№ЮЊACЁЂBCЕФжаЕуЃЌФуФмВТЯыMNЕФГЄЖШТ№ЃПЧыЛГіЭМаЮЃЌаДГіФуЕФНсТлЃЌВЂЫЕУїРэгЩЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌCDЁЭABЃЌДЙзуЮЊDЃЌЕуEдкBCЩЯЃЌEFЁЭABЃЌДЙзуЮЊFЃЎ

(1)CDгыEFЦНааТ№?ЮЊЪВУД?
(2)ШчЙћЁЯ1=ЁЯ2ЃЌЧвЁЯ3=120ЁуЃЌЧѓЁЯACBЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЕФЭјИёжаЃЌAЃЌBЮЊИёЕу
ЃЈЂёЃЉABЕФГЄЕШгк__
ЃЈЂђЃЉЧыгУЮоПЬЖШЕФжБГпЃЌдкШчЭМЫљЪОЕФЭјИёжаЧѓзївЛЕуCЃЌЪЙЕУCA=CBЧвЁїABCЕФУцЛ§ЕШгк![]() ЃЌВЂМђвЊЫЕУїЕуCЕФЮЛжУЪЧШчКЮевЕНЕФ__________________
ЃЌВЂМђвЊЫЕУїЕуCЕФЮЛжУЪЧШчКЮевЕНЕФ__________________

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com