
 的图象上,若A(13,0)、C(8,2),则k的值为( )
的图象上,若A(13,0)、C(8,2),则k的值为( )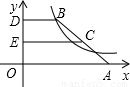
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
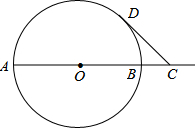 (2013•广州)已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
(2013•广州)已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
 OA交于点F(点D、E、F按顺时针排列),连接DF.设CE=x,OF=y.
OA交于点F(点D、E、F按顺时针排列),连接DF.设CE=x,OF=y.查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(广东广州卷)数学(解析版) 题型:解答题
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O 上运动(不与点B重合),连接CD,且CD=OA.
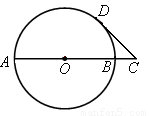
(1)当OC=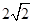 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;
(2)当OC>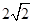 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
①当D为CE中点时,求△ACE的周长;
②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE·ED的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省扬州市广陵区中考二模数学卷(解析版) 题型:解答题
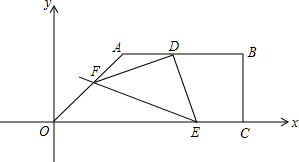
如图,面积为39的直角梯形OABC的直角顶点C在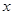 轴上,点C坐标为
轴上,点C坐标为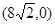 ,AB=
,AB= ,点D是AB边上的一点,且AD:BD=2︰3.有一45°的角的顶点E在
,点D是AB边上的一点,且AD:BD=2︰3.有一45°的角的顶点E在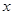 轴上运动,角的一边过点D,角的另一边与直线OA交于点F(点D、E、F按顺时针排列),连结DF.设CE=
轴上运动,角的一边过点D,角的另一边与直线OA交于点F(点D、E、F按顺时针排列),连结DF.设CE=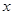 ,OF=
,OF=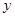 .
.
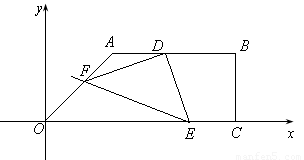
(1)求点D的坐标及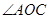 的度数;
的度数;
(2)若点E在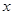 轴正半轴上运动,求
轴正半轴上运动,求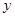 与
与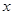 的函数关系式;
的函数关系式;
(3)在点E的运动过程中,是否存在某一时刻,使得△DEF成为等腰三角形?若存在,请求出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com