
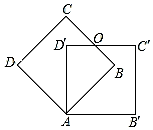
 一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
分析 连接BC′,利用勾股定理的知识求出BC′的长,再根据等腰直角三角形的性质,勾股定理可求BO,OD′,从而可求四边形ABOD′的周长.
解答 解:连接BC′,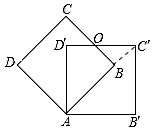
∵旋转角∠BAB′=∠DAD′=45°,
∴B在对角线AC′上,
∵B′C′=AB′=3,
在Rt△AB′C′中,AC′=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴BC′=3$\sqrt{2}$-3,
在等腰Rt△OBC′中,OB=BC′=3$\sqrt{2}$-3,
在直角三角形OBC′中,OC′=$\sqrt{2}$(3$\sqrt{2}$-3)=6-3$\sqrt{2}$,
∴OD′=3-OC′=3$\sqrt{2}$-3,
∴四边形ABOD′的周长是:2AD′+OB+OD′=6+3$\sqrt{2}$-3+3$\sqrt{2}$-3=6$\sqrt{2}$.
故选:B.
点评 本题考查了旋转的性质、正方形的性质以及等腰直角三角形的性质.此题难度适中,注意连接BC′构造等腰Rt△OBC′是解题的关键,注意旋转中的对应关系.


科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 平均数 | C. | 众数 | D. | 中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某种型号节能灯的使用寿命,选择全面调查 | |
| B. | 了解电视剧《人民的名义》的收视率,选择抽样调查 | |
| C. | 端午节期间,国家食品安全检查部门调查市场上粽子的质量情况,选择全面调查 | |
| D. | 对神舟十一号宇宙飞船上某种零部件的检查,选择抽样调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{50}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≤-1 | B. | m≥-1 | C. | m≤1且m≠0 | D. | m≥-1且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
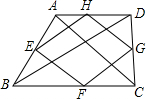 如图,顺次连接四边形ABCD各边中点,得到四边形EFGH,在下列条件中可使四边形EFGH为菱形的是( )
如图,顺次连接四边形ABCD各边中点,得到四边形EFGH,在下列条件中可使四边形EFGH为菱形的是( )| A. | AB=CD | B. | AC=BD | C. | AC丄BD | D. | AD∥BC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com