
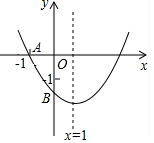
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
分析 ①由抛物线开口向上,对称轴为直线x=1,与y轴的交点B的范围,即可得出a>0、b<0、c<0,进而可得出abc>0,结论①错误;②由抛物线的对称轴以及与x轴的一个交点坐标,可得出另一交点坐标为(3,0),进而可得出9a+3b+c=0,结论②正确;③由点B的范围可得出抛物线顶点纵坐标$\frac{4ac-{b}^{2}}{4a}$<-1,结合a>0可得出4ac-b2<-4a<2a,结论③正确;④由抛物线对称轴为x=1可得出b=-2a,结论④错误.综上即可得出结论.
解答 解:①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),
∴a>0,-$\frac{b}{2a}$=1,c<0,
∴b=-2a<0,
∴abc>0,结论①错误;
②∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,
∴二次函数y=ax2+bx+c(a≠0)的图象与x轴的另一个交点为(3,0),
∴9a+3b+c=0,结论②正确;
③∵二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),
∴抛物线顶点纵坐标$\frac{4ac-{b}^{2}}{4a}$<-1,
∵a>0,
∴4ac-b2<-4a<2a,结论③正确;
④∵抛物线对称轴为直线x=1,
∴-$\frac{b}{2a}$=1,b=-2a,结论④错误.
综上所述,正确的结论有:②③.
故选D.
点评 本题考查了抛物线与x轴的交点、二次函数图象与系数的关系、二次函数的性质以及二次函数图象上点的坐标特征,逐一分析四条结论的正误是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
有一个数值转换器,原理如下:当输入的x为64时,输出的y是( )

A. 8 B. 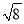 C.
C. 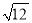 D.
D. 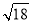
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
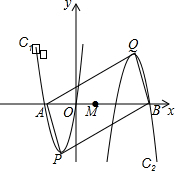 如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.
如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
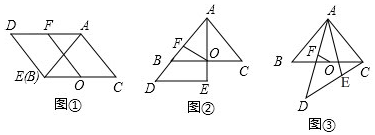
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
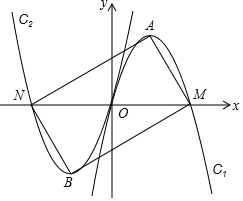 如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2,C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )
如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2,C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )| A. | 2$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
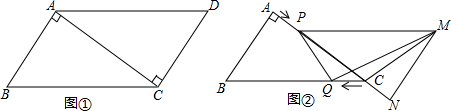
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
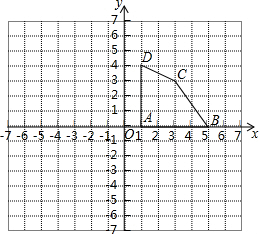 如图,四边形ABCD各顶点的坐标分别为A(1,0),B(5,0),C(3,3),D(1,4).将四边形ABCD先向下平移4个单位长度,再向左平移6个单位长度,得到四边形A′B′C′D′.
如图,四边形ABCD各顶点的坐标分别为A(1,0),B(5,0),C(3,3),D(1,4).将四边形ABCD先向下平移4个单位长度,再向左平移6个单位长度,得到四边形A′B′C′D′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com