

分析 (1)求出直线AC的解析式,用m表示点F、点G坐标,根据二次函数即可解决问题,注意自变量的取值范围.
(2)分三种情形列方程解决问题①如图②中,当AP为斜边时,作PF⊥DE于F;②如图③中,PQ为斜边时,作PF⊥OA于F;③当AQ为斜边时,作PF⊥OA于F,QH⊥FP于H.
(3)分两种情形想办法列出方程解决①如图⑤中,当MN<BN时,作NF⊥TK于F;②如图⑥中,当MN>BN时,作NF⊥TK于F.
解答 解:(1)如图①中,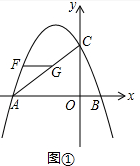
∵y=-$\frac{\sqrt{3}}{12}$x2-x+3$\sqrt{3}$,
令x=0,y=3$\sqrt{3}$,
令y=0,-$\frac{\sqrt{3}}{12}$x2-x+3$\sqrt{3}$=0,解得x=2$\sqrt{3}$或-6$\sqrt{3}$,
∴A(-6$\sqrt{3}$,0),B(2$\sqrt{3}$,0),C(0,3$\sqrt{3}$),
∴直线AC解析式为y=$\frac{1}{2}$x+3$\sqrt{3}$,
设F(m,-$\frac{\sqrt{3}}{12}$x2-m+3$\sqrt{3}$),
∵FG∥AB,
∴G(-$\frac{\sqrt{3}}{6}$m2-2m,-$\frac{\sqrt{3}}{12}$m2-m+3$\sqrt{3}$),
∴FG=-$\frac{\sqrt{3}}{6}$m2-3m=-$\frac{\sqrt{3}}{6}$(m+3$\sqrt{3}$)2+$\frac{9\sqrt{3}}{2}$,
∵-6$\sqrt{3}$<m<-4$\sqrt{3}$,
∴m=-4$\sqrt{3}$时,FG有最大值,最大值为4$\sqrt{3}$.
(2)∵y=-$\frac{\sqrt{3}}{12}$(x+2$\sqrt{3}$)2+4$\sqrt{3}$,
∴顶点D坐标(-2$\sqrt{3}$,4$\sqrt{3}$),对称轴x=-2$\sqrt{3}$,
①如图②中,当AP为斜边时,作PF⊥DE于F,
设P(t,-$\frac{\sqrt{3}}{12}$t2-t+3$\sqrt{3}$),t<-6$\sqrt{3}$,
∵∠AQP=90°,
∴∠AQE+∠PQF=90°,∠PQF+∠QPF=90°,
∴∠AQE=∠QPF,∵∠AEQ=∠PFQ,AQ=PQ,
∴△AEQ≌△QFP,
∴QF=AE=4$\sqrt{3}$,EQ=PF=-t,
∴EF=EQ+QF=4$\sqrt{3}$-t,
∴-$\frac{\sqrt{3}}{12}$t2-t+3$\sqrt{3}$=-4$\sqrt{3}$+t,
∴t=-4$\sqrt{3}$-2$\sqrt{33}$或-4$\sqrt{3}$+2$\sqrt{33}$(舍弃),
②如图③中,PQ为斜边时,作PF⊥OA于F,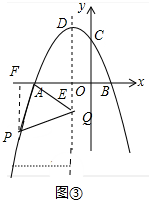
由△PFA≌△AEQ,
∴PF=AE=4$\sqrt{3}$,
∴-$\frac{\sqrt{3}}{12}$t2-t+3$\sqrt{3}$=-4$\sqrt{3}$,
解得t=-2$\sqrt{3}$-4$\sqrt{6}$或-2$\sqrt{3}$+4$\sqrt{6}$(舍弃),
③当AQ为斜边时,作PF⊥OA于F,QH⊥FP于H,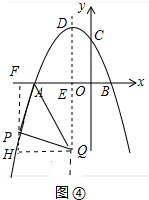
由△AFP≌△PHQ,
∴QH=PF,
∴-$\frac{\sqrt{3}}{12}$t2-t+3$\sqrt{3}$=t,
解得t=-4$\sqrt{3}$-2$\sqrt{21}$或-4$\sqrt{3}$+2$\sqrt{21}$(舍弃),
综上所述,满足条件的点P坐标为(-2$\sqrt{3}$-4$\sqrt{6}$,-4$\sqrt{3}$)或(-4$\sqrt{3}$-2$\sqrt{21}$,-4$\sqrt{3}$-2$\sqrt{21}$)或(-4$\sqrt{3}$-2$\sqrt{33}$,-8$\sqrt{3}$-2$\sqrt{33}$).
(3)①如图⑤中,当MN<BN时,作NF⊥TK于F.
∵A(-6$\sqrt{3}$,0),B(2$\sqrt{3}$,0),∠OAM=30°,
∴OM=6,AM=16,M(0,-6),
∵AS=SM,
∴OS=SM=OM=6,
∴△OSM是等边三角形,设MN=m,
∵tan∠OBM=$\frac{OM}{OB}$=$\frac{\sqrt{3}}{3}$,
∴∠OBM=60°,
∴∠AMB=90°,
∵△SOT≌△SMN,
∴∠SOT=∠SMN=90°,
∵∠AOS=30°,
∴∠TOA=60°
∴∠BOK=∠OBK=60°,
∴△OBK是等边三角形,
∴OK=BK,
∵∠KOM=∠OMK=30°,
∴OK=KM=KB,
∵TO=MN=m,
∴TK=TO+OK=2$\sqrt{3}$+m,NK=MK-MN=2$\sqrt{3}$-m,
∴NF=$\frac{\sqrt{3}}{2}$NK,
∵S△KTN=$\frac{1}{12}$S△ABM,
∴$\frac{1}{2}$•(2$\sqrt{3}$+m)•$\frac{\sqrt{3}}{2}$•(2$\sqrt{3}$-m)=$\frac{1}{12}$•$\frac{1}{2}$•8$\sqrt{3}$•6,
∴m=2或-2(舍弃),
∴MN=2.
②如图⑥中,当MN>BN时,作NF⊥TK于F.
同理可得,OT=MN=m,OK=2$\sqrt{3}$,TK=2$\sqrt{3}$+m,NK=MN-MK=m-2$\sqrt{3}$,NF=$\frac{\sqrt{3}}{2}$NK,
∵S△KTN=$\frac{1}{12}$S△ABM,
∴$\frac{1}{2}$•(m+2$\sqrt{3}$)•$\frac{\sqrt{3}}{2}$(m-2$\sqrt{3}$)=2$\sqrt{3}$,
解得m=2$\sqrt{5}$或-2$\sqrt{5}$(舍弃).
综上所述,MN的长为2或2$\sqrt{5}$.
点评 本题考查二次函数综合题、一次函数、旋转变换、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会分类讨论,注意不能漏解,属于中考压轴题.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:选择题
| A. | 若a=b,则ac-3=bc-3 | B. | 若a=b,则$\frac{a}{c^2+1}$=$\frac{b}{c^2+1}$ | ||
| C. | 若x=3,则x2=3x | D. | 若ax=bx,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
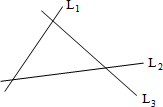 现有三条公路L1、L2、L3交汇成三角形的地方,在此处要修建一个加油站服务区,以方便司机休息加油.此加油站的位置要到三条公路的距离相等,请你画出表示此加油站的位置P.
现有三条公路L1、L2、L3交汇成三角形的地方,在此处要修建一个加油站服务区,以方便司机休息加油.此加油站的位置要到三条公路的距离相等,请你画出表示此加油站的位置P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
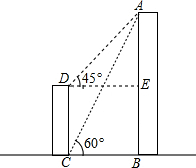 如图,AB、CD为两栋建筑物,建筑物CD的高度为20m,从建筑物CD的顶部D点测得建筑物AB的顶部A点的仰角为45°,从建筑物CD的底部C点测得建筑物AB的顶部A点的仰角60°,求建筑物AB的高度(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,AB、CD为两栋建筑物,建筑物CD的高度为20m,从建筑物CD的顶部D点测得建筑物AB的顶部A点的仰角为45°,从建筑物CD的底部C点测得建筑物AB的顶部A点的仰角60°,求建筑物AB的高度(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com