
【题目】某市居民生活用水实行“阶梯水价”收费,具体收费标准见下表:
每户每月用水量 | 水的价格(单位:元/吨) |
不超过20吨的部分 | 1.6 |
超过20吨且不超过30吨的部分 | 2.4 |
超过30吨的部分 | 3.3 |
例:甲用户1月份用水25吨,应缴水费![]() (元).
(元).
(1)若乙用户1月份用水10吨,则应缴水费________元;
(2)若丙用户1月份应缴水费62.6元,则用水________吨;.
(3)若丁用户1、2月份共用水60吨(1月份用水量超过了2月份),设2月份用水![]() 吨,求丁用户1、2月份各应缴水费多少元.(用含
吨,求丁用户1、2月份各应缴水费多少元.(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)16;(2)32; (3) 1月份应缴水费![]() 元.当2月份用水量不超过20吨时,应缴水费1.6
元.当2月份用水量不超过20吨时,应缴水费1.6![]() 元;当2月份用水量超过20吨但不超过30吨时,应缴水费
元;当2月份用水量超过20吨但不超过30吨时,应缴水费![]() 元.
元.
【解析】
(1)根据每户每月用水量不超过20时,水费价格为1.6元/吨,可知乙用户1月份用水10吨,则应缴水费:1.6×10,计算即可;(2)由于用水30吨时应缴水费为:1.6×20+2.4×10=56<62.6,所以丙用户1月份用水超过30吨,列出方程,求解即可;(3)由丁用户1、2两个月共用水60吨,设2月份用水![]() 吨,则1月份用水(60-a)吨,根据1月份用水量超过了2月份,得出1月份用水量超过了2月份,得出1月份用水量大于30吨,2月份用水量小于30吨,根据三级收费求出1月份应缴水费,分两种情况求出2月份应缴水费,①当2月份用水量不超过20吨时;②当2月份用水量超过20吨但不超过30吨时;
吨,则1月份用水(60-a)吨,根据1月份用水量超过了2月份,得出1月份用水量超过了2月份,得出1月份用水量大于30吨,2月份用水量小于30吨,根据三级收费求出1月份应缴水费,分两种情况求出2月份应缴水费,①当2月份用水量不超过20吨时;②当2月份用水量超过20吨但不超过30吨时;
解:(1)依题意得:1.6×10=16;
故答案为:16
(2) 依题意得:由于用水30吨时应缴水费为:1.6×20+2.4×10=56<62.6,所以丙用户1月份用水超过30吨,设用水为x吨,依题意得:![]()
解得:x=32
故答案为:32;
(3)因为1月份用水量超过了2月份,所以1月份用水量超过了30吨,2月份用水量少于30吨.1月份应缴水费![]() 元.
元.
①当2月份用水量不超过20吨时,应缴水费1.6![]() 元;
元;
②当2月份用水量超过20吨但不超过30吨时,应缴水费![]() 元.
元.


科目:初中数学 来源: 题型:
【题目】如图:图形都是由面积为1的正方形按一定的规律组成,其中第(1)个图形中面积为1的正方形有9个,第(2)个图形中面积为1的正方形有14个,…,按此规律.则第(9)个图形中面积为1的正方形的个数为( )
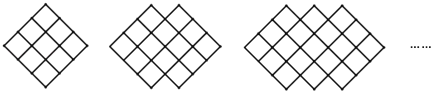
A.49B.45C.54D.50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如下所示的统计表和如图所示的统计图.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
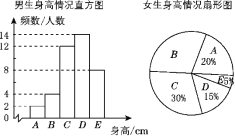
根据图表中提供的信息,回答下列问题:
(1)女生身高在B组的有________人;
(2)在样本中,身高在150≤x<155之间的共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时生产一种零件,在5天中,两台机床每天出次品的数量如下表:
甲 | 0 | 1 | 2 | 0 | 2 |
乙 | 2 | 1 | 0 | 1 | 1 |
关于以上数据的平均数、中位数、众数和方差,说法不正确的是
A. 甲、乙的平均数相等B. 甲、乙的众数相等
C. 甲、乙的中位数相等D. 甲的方差大于乙的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
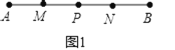
【题目】如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;
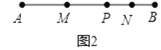
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, AC=4.5cm. M是边AC上的一个动点,连接MB,过点M作MB的垂线交AB于点N. 设AM=x cm,AN=y cm.(当点M与点A或点C重合时,y的值为0)
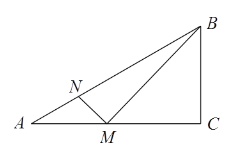
探究函数y随自变量x的变化而变化的规律.
(1) 通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 1.7 | 1.6 | 1.2 | 0 |
(要求:补全表格,相关数值保留一位小数)
(2)建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当AN=![]() AM时,AM的长度约为 cm(结果保留一位小数).
AM时,AM的长度约为 cm(结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018春季环境整治活动中,某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com