
【题目】已知抛物线过A(-1,0),B(3,0)两点,与y轴交于C点,且BC=3![]() ,则这条抛物线的解析式为 ( )
,则这条抛物线的解析式为 ( )
A. y=-x2+2x+3 B. y=x2-2x-3
C. y=x2+2x―3或y=-x2+2x+3 D. y=-x2+2x+3或y=x2-2x-3
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】红红有5张写着以下数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1) 从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是_________
(2) 从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是_________
(3) 从中取出除0以外的其他4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使运算结果为24(注:每个数字只能用一次,如:23×[1-(-2)],请另外写出两种符合要求的运算式子:_________________ _________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里(将各数用逗号分开):
+8,0.275,-|-2|,0,-1.04,-(-10),![]() ,
,![]() ,
,![]() ,0.1.
,0.1.
正整数:﹛ …﹜
整数:﹛ …﹜
负有理数: ﹛ …﹜
分数: ﹛ …﹜
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据: ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的.点O′在x轴的正半轴上,点B的坐标为(1,3).
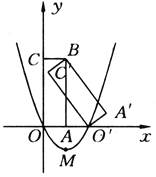
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O,O′两点,且图象顶点M的纵坐标为-l,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
(3)求边C′O′所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A. B为数轴上两点,AB=15,且OA:OB=2.
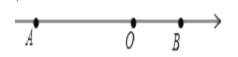
(1)A、B对应的数分别为___、___;
(2)点A. B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A. B相距1个单位长度?
(3)点A. B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得4AP+3OBmOP为定值,若存在请求出m值以及这个定值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
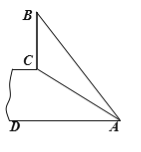
【题目】如图,斜坡AC的坡度(坡比)为1: ![]() ,AC=10米.坡顶有一垂直于水平面的旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.
,AC=10米.坡顶有一垂直于水平面的旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
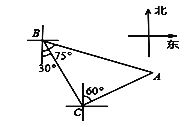
【题目】轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.50B.25C.25![]() D.25
D.25![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com