练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
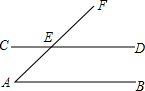
    2．如图，直线AB∥CD，AF交CD于点E，∠CEA=45°，则∠A等于（　　）
    A．35°B．45°C．50°D．135°

    分析 根据两直线平行，内错角相等解答即可．

    解答 解：∵AB∥CD，
    ∴∠A=∠CEA，
    ∵∠CEA=45°，
    ∴∠A=45°．
    故选B．

    点评 本题考查了平行线的性质，是基础题，熟记性质并准确识图是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．已知函数y=x2+3kx+k+1的图象的顶点在y轴上，那么函数的关系式是y=x2+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．有如下命题：1有理数与数轴上的点一一对应；2无理数包括正无理数，0，负无理数；3如果一个数的平方根是这个数本身，那么这个数是1或0；4一个实数的立方根不是正数就是负数．其中错误的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

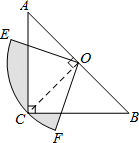    10．如图，在△ABC中∠C=90°，AC=BC=2，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形OEF，弧EF经过点C，则图中阴影部分的面积为$\frac{1}{2}$π-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解不等式组：$\left\{\begin{array}{l}{4x＞2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$，并把不等式组的解集表示在数轴上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．若关于a的方程（a-1）x2+x+a2-2a-1=0的一根为-1，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

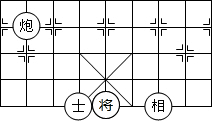    14．中国象棋在中国有着三千多年的历史，它难易适中，趣味性强，变化丰富细腻，棋盘棋子文字都体现了中国文化．如图，如果所在位置的坐标为（-1，-1），所在位置的坐标为（2，-1），那么，所在位置的坐标为（-3，2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

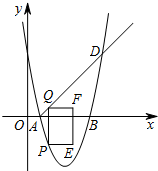    11．如图，在平面直角坐标系中，抛物线y=ax2+bx+5与x轴交于A（1，0）、B（5，0）两点，点D是抛物线上横坐标为6的点．点P在这条抛物线上，且不与A、D两点重合，过点P作y轴的平行线与射线AD交于点Q，过点Q作QF垂直于y轴，点F在点Q的右侧，且QF=2，以QF、QP为邻边作矩形QPEF．设矩形QPEF的周长为d，点P的横坐标为m．
    （1）求这条抛物线所对应的函数表达式．
    （2）求这条抛物线的对称轴将矩形QPEF的面积分为1：2两部分时m的值．
    （3）求d与m之间的函数关系式及d随m的增大而减小时d的取值范围．
    （4）当矩形QPEF的对角线互相垂直时，直接写出其对称中心的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解方程：$\frac{4+x}{x-1}-5=\frac{2x}{x+1}$．

    查看答案和解析>>

    同步练习册答案