
 时,求y与x的函数关系式;
时,求y与x的函数关系式;
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:不详 题型:解答题
 的半径为1,以
的半径为1,以 为原点,建立如图所示的直角坐标系.有一个正方形
为原点,建立如图所示的直角坐标系.有一个正方形 ,顶点
,顶点 的坐标为(
的坐标为( ,0),顶点
,0),顶点 在
在 轴上方,顶点
轴上方,顶点 在⊙
在⊙ 上运动.
上运动.
 运动到与点
运动到与点 、
、 在一条直线上时,
在一条直线上时,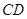 与⊙
与⊙ 相切吗?如果相切,请说明理由,并求出
相切吗?如果相切,请说明理由,并求出 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由; 的横坐标为
的横坐标为 ,正方形
,正方形 的面积为
的面积为 ,求出
,求出 与
与 的函数关系式,并求出
的函数关系式,并求出 的最大值和最小值.
的最大值和最小值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (米)与注水时间
(米)与注水时间 (小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
(小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
 (米)与注水时间
(米)与注水时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (微克)随时间
(微克)随时间 (小时)的变化如图所示,那么成年人按规定剂量服药后:
(小时)的变化如图所示,那么成年人按规定剂量服药后:
 与
与 之间的函数关系式.
之间的函数关系式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com