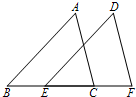
如图.△DEF是将△ABC沿射线BC的方向平移后得到的．若BC=5.EC=3.则CF的长为( )A．2B．3C．5D．8 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

17．

如图，△DEF是将△ABC沿射线BC的方向平移后得到的．若BC=5，EC=3，则CF的长为（　　）

A．

B．

C．

D．

分析根据平移的性质，结合图形，可直接求得结果．

解答解：根据图形可得：线段BE的长度即是平移的距离，
又BC=5，EC=3，
∴BE=5-3=2．
故选A；

点评本题考查了平移的性质，解题的关键是理解平移的方向，由图形判断平移的方向和距离．注意结合图形解题的思想．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

7．

如图，已知AD∥BC，AE平分∠BAD，CD与AE相交于点F，∠CFE=∠E，试说明AB∥DC，把下面的说理过程补充完整．
∵AD∥BC（已知）
∴∠2=∠E（两直线平行，内错角相等）
∵AE平分∠BAD（已知）
∴∠1=∠2　（角平分线的定义）
∴∠1=∠E（等量代换）
∵∠CFE=∠E（已知）
∴∠1=∠CFE
∴AB∥CD（同位角相等，两直线平行）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

8．若反比例函数$y=\frac{k}{x}$的图象经过点（1，4），则它的图象也一定经过的点是（　　）

A．

（-1，-4）

B．

（1，-4）

C．

（4，-1）

D．

（-1，4）

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

5．

如图，在Rt△ABC中，∠ABC=90°，AB=BC=$2\sqrt{2}$，将△ABC绕点A逆时针旋转60°，得到△ADE，连接BE，则BE的长是2$\sqrt{3}$+2．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．探索：在图1至图2中，已知△ABC的面积为a，
（1）如图1，延长△ABC的边BC到点D，使CD=BC，连接DA；延长边CA到点E，使CA=AE，连接DE；若△DCE的面积为S₁，则S₁=2a（用含a的代数式表示）；
（2）在图1的基础上延长AB到点F，使BF=AB，连接FD，FE，得到△DEF （如图2）．若阴影部分的面积为S₂，则S₂=6a （用含a的代数式表示）；
（3）发现：像上面那样，将△ABC各边均顺次延长一倍，连接所得端点，得到△DEF（如图2），此时，我们称△ABC向外扩展了一次．可以发现，扩展n次后得到的三角形的面积是△ABC面积的7ⁿ倍（用含n的代数式表示）；
（4）应用：某市准备在市民广场一块足够大的空地上栽种牡丹花卉，工程人员进行了如下的图案设计：首先在△ABC的空地上种紫色牡丹，然后将△ABC向外扩展二次（如图3）．在第一次扩展区域内种黄色牡丹，第二次扩展区域内种紫色牡丹，紫色牡丹花的种植成本为100元/平方米，黄色牡丹花的种植成本为95元/平方米．要使得种植费用不超过48700元，工程人员在设计时，三角形ABC的面积至多为多少平方米？