
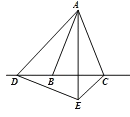
【题目】在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.
(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;
(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;
(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.

【答案】(1)α+β=180°,理由见解析;(2)α=β,理由见解析;(3)α=β
【解析】
(1)如图①,根据等式的性质就可以得出∠CAE=∠BAD,就可以得出△ABD≌△ACE就可以得出∠ABD=∠ACE,由三角形的内角和定理就可以得出结论;
(2)如图②,根据等式的性质就可以得出∠CAE=∠BAD,就可以得出△ABD≌△ACE就可以得出∠ABD=∠ACE,就可以得出结论;
(3)根据条件画出图形③,根据等式的性质就可以得出∠CAE=∠BAD,就可以得出△ABD≌△ACE就可以得出∠ABD=∠ACE,由外角与内角的关系就可以得出结论.
解:(1)α+β=180°
理由:∵∠DAE=∠BAC,
∴∠DAE-∠CAD=∠BAC-∠CAD,
即∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS) ,
∴∠ABD=∠ACE,
在△ABC中,
∵∠BAC+∠ABC+∠ACB=180°,∠ABC=∠ACE,
∴∠BAC+∠ACB+∠ACE=180°,
∵∠ACB+∠ACE=∠DCE=β,
∴α+β=180°;
(2)α=β
理由:∵∠DAE=∠BAC,
∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS).
∴∠ABD=∠ACE.
∵∠ABC+∠BAC+∠ACB=180°,∠ACB+∠ACD=180°,
∴∠ACD=∠ABC+∠BAC=∠ACE+∠ECD.
∴∠BAC=∠ECD.
∴α=β.
(3)α=β.
 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图(1)所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:

(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、图(1)XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;
②如图(3)DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;(写出解答过程)
③如图(4),∠ABD,∠ACD的10等分线相交于点G1、G2![]() 、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.
、G9,若∠BDC=140°,∠BG1C=77°,则∠A的度数=__________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,D为AB上一点,连接CD.
(1)如图1,若∠BCA=90°,CD⊥AB,则![]() =______(直接写出结果).
=______(直接写出结果).
(2)如图2,若BD=AC,E为CD的中点,AE与BC存在怎样的数量关系,判断并说明理由;
(3)如图3,CD平分∠ACB,BF平分∠ABC,交CD于F.若BF=AC,求∠ACD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D,E,F分别在三边上,且BE=CD,BD=CF,G为EF的中点.
(1)若∠A=40°,求∠B的度数;
(2)试说明:DG垂直平分EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接济川中学红歌演讲比赛,济川校区七年级(15)(16)班决定订购同一套服装,两班一共有103人(15班人数多于16班),经协商,某服装店给出的价格如下:
购买人数/人 | 1~50人 | 50~100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
例如:若购买人数为60人,则购买共需花费60×45=2700元.
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么15,16班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB∥CD,∠BCF=180°,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.
求证:AC⊥BD

请将下列证明过程中的空格补充完整.
证明:∵AB∥CD,
∴∠ABC=∠DCF.(_____)
∵BD平分∠ABC,CE平分∠DCF,
∴∠2=![]() ∠ABC,∠4=
∠ABC,∠4=![]() ∠DCF.(_____)
∠DCF.(_____)
∴_______.
∴BD∥CE.(_______)
∴______.(两直线平行,内错角相等)
∵∠ACE=90°,
∴∠BGC=90°,即AC⊥BD.(_____)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”
概念理解:如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)
(1)∠ABO的度数为 ,△AOB (填“是”或“不是”)“和谐三角形”;
(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.
应用拓展:如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°以AB为直径的⊙O交AB于点D,点E为BC的中点,连接DE.
(1)求证:DE是⊙O的切线.
(2)若∠BAC=30°,DE=3,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com