
【题目】(本小题满分9分)已知点D是![]() 边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
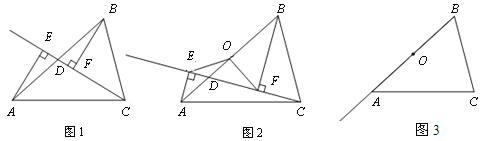
(1)如图1,当点D与点O重合时,AE与BF的位置关系是____________,OE与OF的数量关系是__________;
(2)如图2,当点D在线段AB上不与点O重合时,试判断OE与OF的数量关系,并给予证明;
(3)如图3,当点D在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路. (备注:直角三角形中,斜边上的中线等于斜边的一半)
【答案】见解析
【解析】(1)AE∥BF,OE=OF.
如图,
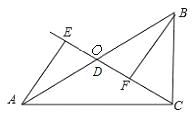
当点D与点O重合时,AE与BF的位置关系是AE∥BF,OE与OF的数量关系是OE=OF.
理由是:∵O为AB的中点,
∴AO=BO,
∵AE⊥CD,BF⊥CO,
∴AE∥BF,∠AEO=∠BFO=90°,(2分)
在![]() 和
和![]() 中
中
∠AOE=∠BOF,∠AEO=∠BFO,AO=BO,
∴△AEO≌△BFO,
∴OE=OF,
故答案为:AE∥BF,OE=OF(3分)
(2)结论:OE=OF. (4分)
证明:如图,延长EO交BF于G.
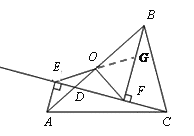
∵AE∥BF,
∴∠AEO=∠BGO,
在![]() 和
和![]() 中,
中,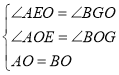 ,
,
∴△AEO≌△BGO(ASA).∴OE=OG.
∵BF⊥CD,∴FO是![]() 斜边上的中线,
斜边上的中线,
∴OE=OF=OG,
即OE=OF.(6分)
(3)(2)中的结论仍然成立. (7分)
所画图形如图所示,
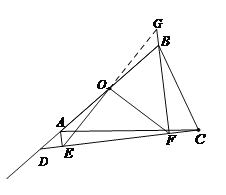 (8分)
(8分)
证明思路:延长EO、FB交于G.
由(2)的证明思路可以得到△AOE≌△BOG,由全等得到OE=OG;由BF⊥CD,得到FO是![]() 斜边GE上的中线;可得到OE=OF.(9分)
斜边GE上的中线;可得到OE=OF.(9分)


科目:初中数学 来源: 题型:
【题目】一水塘里有鲤鱼、鲫鱼、鲢鱼共10 000尾,一渔民通过多次捕捞实验后发现,鲤鱼、鲫鱼出现的频率分别是31%和42%,则这个水塘里大约有鲢鱼尾.
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 有理数包括整数和分数;
B. 一个代数式不是单项式就是多项式;
C. 几个有理数相乘,若负因数的个数是偶数个,则积为正数;
D. 绝对值等于它本身的数是0、1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.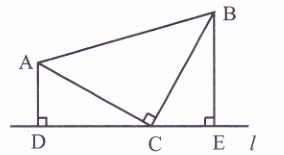
(2)如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)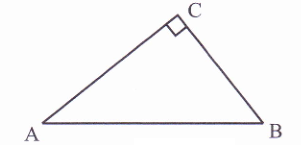
(3)若AB=10,CD=3,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个圆柱体的侧面展开图为长方形ABCD,若AB=6.28cm,BC=18.84cm,则该圆柱体的体积是多少?(π取3.14,结果精确到十分位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:
①AD⊥BD;②∠AOC=∠ABC;③CB平分∠ABD;④AF=DF;⑤BD=2OF.
其中一定成立的是( )

A.①③⑤ B.②③④ C.②④⑤ D.①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com