
分析 首先根据有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,判断出有理数、无理数各有哪些;然后根据正数都大于0,负数都小于0,判断出正数、负数各有哪些即可.
解答 解:有理数集合:{$\frac{22}{7}$、0.314、0.313131…、$\root{3}{8}$、-$\sqrt{64}$、…};
无理数集合:{$\frac{π}{5}$、-$\sqrt{5}$、7.151551…、…};
正数集合:{$\frac{22}{7}$、$\frac{π}{5}、$0.314、0.313131…、$\root{3}{8}$、7.151551…、…};
负数集合:{-$\sqrt{5}$、-$\sqrt{64}$、…}.
故答案为:$\frac{22}{7}$、0.314、0.313131…、$\root{3}{8}$、-$\sqrt{64}$;
$\frac{π}{5}$、-$\sqrt{5}$、7.151551…;
$\frac{22}{7}$、$\frac{π}{5}、$0.314、0.313131…、$\root{3}{8}$、7.151551…;
-$\sqrt{5}$、-$\sqrt{64}$.
点评 此题主要考查了实数的定义和分类,要熟练掌握,解答此题的关键是要明确:(1)有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.(2)正数都大于0,负数都小于0.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
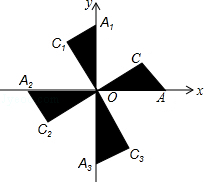 如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OAC,Rt△OA1C1,Rt△OA2C2,…的斜边都在坐标轴上,∠AOC=∠A1OC1=∠A2OC2=∠A3OC3=…=30°.若点A的坐标为(3,0),OA=OC1,OA1=OC2,OA2=OC3,…则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ | C. | $-3×{(\frac{{2\sqrt{3}}}{3})^{2014}}$ | D. | $3×{(\frac{{2\sqrt{3}}}{3})^{2015}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>b | B. | y2>b>y1 | C. | y2>0>y1 | D. | y1>b>y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com