
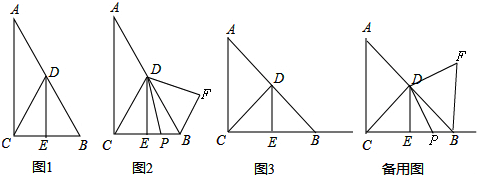
分析 (1)在Rt△ABC中,∠ACB=90°,D是AB的中点,DE⊥BC于E,∠A=30°,所以∠CDE=30°,所以DE=$\sqrt{3}$EC;
(2)根据条件证明△DCP≌△DBF进而可证BF+BP=BC,在Rt△CDE中,利用特殊角的三角函数值可得BC=2CE=$\frac{2\sqrt{3}}{3}$DE,所以BF+BP=$\frac{2\sqrt{3}}{3}$DE;
(3)分两种情况讨论:点P在线段CB上时,BF+BP=2DE,点P在CB延长线时,BF-BP=2DE.
解答 解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°.
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形.
∵DE⊥BC,
∴DE=$\frac{\sqrt{3}}{2}$BC,
故答案为DE=$\frac{\sqrt{3}}{2}$BC.
(2)BF+BP=$\frac{2\sqrt{3}}{3}$DE.
理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF.
∵∠CDB=60°,
∴∠CDB-∠PDB=∠PDF-∠PDB.
∴∠CDP=∠BDF.
在△DCP和△DBF中,∵DC=DB,∠CDP=∠BDF,DP=DF,
∴△DCP≌△DBF(SAS),
∴CP=BF.
∵CP=BC-BP,
∴BF+BP=BC.
∵由(1)DE=$\frac{\sqrt{3}}{2}$BC,
∴BC=$\frac{2\sqrt{3}}{3}$DE.
∴BF+BP=$\frac{2\sqrt{3}}{3}$DE.
(3)①点P在CB延长线时,如图,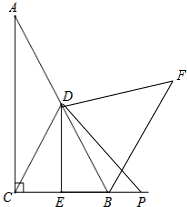
与(2)一样可证明△DCP≌△DBF,
∴CP=BF.
∵CP=BC+BP,
∴BF-BP=BC=2DE.
②点P在线段CB上时,如图,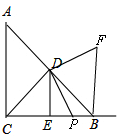
与(2)一样可证明△DCP≌△DBF,
∴CP=BF.
∵CP=BC-BP,
∴BF+BP=BC=2DE.
∴DE、BF、BP三者之间的数量关系为BF-BP=2DE,或BF+BP=2DE.
点评 此题是几何变换综合题,主要考查了直角三角形的性质、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是深入观察图形,准确找出图形中隐含的数量关系,正确运用直角三角形的性质、全等三角形的判定及其性质等几何知识点来分析、判断、推理或解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
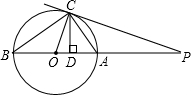 如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
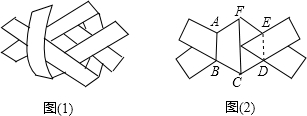 用两条宽均为2cm的纸条(假设纸条的长度足够长),折叠穿插,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正六边形ABCDEF,则折出的正六边形的边长为$\frac{4\sqrt{3}}{3}$cm.
用两条宽均为2cm的纸条(假设纸条的长度足够长),折叠穿插,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正六边形ABCDEF,则折出的正六边形的边长为$\frac{4\sqrt{3}}{3}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com