
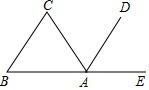
 如图,已知A、B、E三点在同一直线上,直线AD平分角∠EAC,AD∥BC,∠B=60°,求∠C的度数.
如图,已知A、B、E三点在同一直线上,直线AD平分角∠EAC,AD∥BC,∠B=60°,求∠C的度数. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
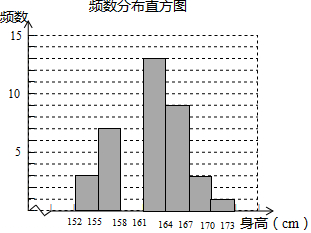 某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.| 身高分组 | 频数 | 频率 |
| 152≤x<155 | 3 | 0.06 |
| 155≤x<158 | 7 | 0.14 |
| 158≤x<161 | m | 0.28 |
| 161≤x<164 | 13 | n |
| 164≤x<167 | 9 | 0.18 |
| 167≤x<170 | 3 | 0.06 |
| 170≤x<173 | 1 | 0.02 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 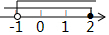 | B. | 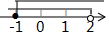 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
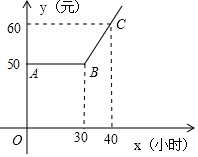 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
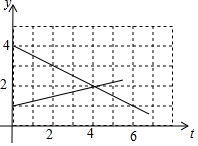 某工厂有甲、乙两个长方体的水池,甲水池较深,甲池的水用抽水机匀速地抽入乙池,如图所示的是甲、乙两个水池水的深度y(m)与抽水时间t(h)的函数关系的图象.
某工厂有甲、乙两个长方体的水池,甲水池较深,甲池的水用抽水机匀速地抽入乙池,如图所示的是甲、乙两个水池水的深度y(m)与抽水时间t(h)的函数关系的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com