
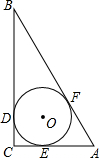
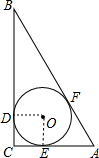
 如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm.
如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm.| 60 |
| 17 |
| OD |
| BC |
| AD |
| AC |
| r |
| 5 |
| 12-r |
| 12 |
| 60 |
| 17 |
| 60 |
| 17 |
| AC2+BC2 |
| 60 |
| 17 |
| OD |
| BC |
| AD |
| AC |
| r |
| 5 |
| 12-r |
| 12 |
| 60 |
| 17 |
| 60 |
| 17 |


科目:初中数学 来源: 题型:
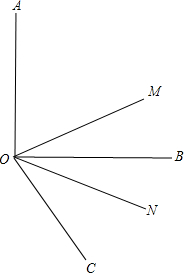 如图,射线OC在∠AOB的外部,∠BOC=a(a为锐角)且OM平分∠AOC,ON平分∠BOC.
如图,射线OC在∠AOB的外部,∠BOC=a(a为锐角)且OM平分∠AOC,ON平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:
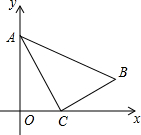 如图,△ABC中,A,B,C三点的坐标分别是A(0,
如图,△ABC中,A,B,C三点的坐标分别是A(0,| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 甲,乙两人在直线跑道上同起点,同终点,同方向匀速跑步500m,先到终点的人原地休息,已知甲先出发2秒,在在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,
甲,乙两人在直线跑道上同起点,同终点,同方向匀速跑步500m,先到终点的人原地休息,已知甲先出发2秒,在在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,查看答案和解析>>
科目:初中数学 来源: 题型:
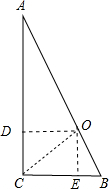
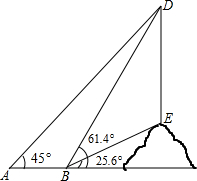 如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com