

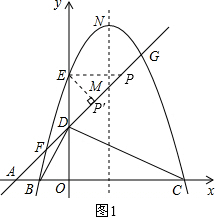
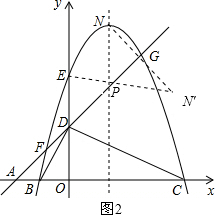
 ����3�������ı���PMNQΪƽ���ı���ʱ����P����Ϊ
����3�������ı���PMNQΪƽ���ı���ʱ����P����Ϊ �������ı���PMNQΪ��������ʱ����P���� Ϊ
�������ı���PMNQΪ��������ʱ����P���� Ϊ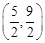 .
.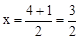 .
.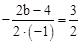 ��c-5=4����� b=2��c=9.
��c-5=4����� b=2��c=9. .
. ����N������
����N������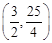 ����MN=
����MN=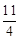 .
.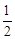 ��x2=
��x2=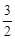 ��
��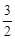 ʱ����P�����M�غϣ�
ʱ����P�����M�غϣ�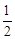 ʱ����P��������
ʱ����P�������� .
.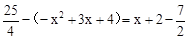 ����ã�x=
����ã�x=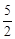 .
.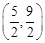 ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��
��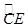 �������֤����Ľ��ۣ�
�������֤����Ľ��ۣ�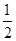 AE���Ƿ���ڹ���M��ֱ�ߣ�ʹ��ֱ���루1�������õ������ߵ��������㵽y��ľ�����ȣ������ڣ��������ֱ�߶�Ӧ�����Ľ���ʽ���������ڣ���˵�����ɣ�
AE���Ƿ���ڹ���M��ֱ�ߣ�ʹ��ֱ���루1�������õ������ߵ��������㵽y��ľ�����ȣ������ڣ��������ֱ�߶�Ӧ�����Ľ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
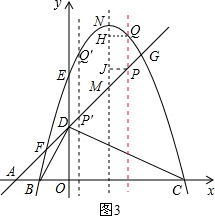
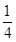 (5m2��2m+13)="0" (mΪ����)������ʵ��������M���������ϣ�����MQ��MH��PM���ң�MPƽ�֡�QMH�����tֵ����M�����꣮
(5m2��2m+13)="0" (mΪ����)������ʵ��������M���������ϣ�����MQ��MH��PM���ң�MPƽ�֡�QMH�����tֵ����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
| ���۵���x ��Ԫ/���� | �� | 55 | 60 | 70 | 75 | �� |
| һ�ܵ�������y ������ | �� | 450 | 400 | 300 | 250 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
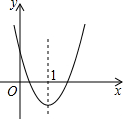
| A��a>0 | B��c>0 | C��b2-4ac>0 | D��a+b+c>0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
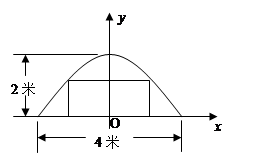
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 .����ֱ�ǡ�EFG�У�EF=4�� ��EGF=45��,�ҡ�EFG���ABCDλ��ֱ��AD��ͬ�࣬��F���D�غϣ�GF��AD��ͬһֱ���ϣ���EFG�ӵ�D������ÿ��1����λ���ٶ�������DA����ƽ�ƣ�����G����Aʱֹͣ�˶���ͬʱ��PҲ�ӵ�A��������ÿ��3����λ���ٶ�������AD��DC�����˶��������Cʱֹͣ�˶������˶���ʱ��Ϊt.
.����ֱ�ǡ�EFG�У�EF=4�� ��EGF=45��,�ҡ�EFG���ABCDλ��ֱ��AD��ͬ�࣬��F���D�غϣ�GF��AD��ͬһֱ���ϣ���EFG�ӵ�D������ÿ��1����λ���ٶ�������DA����ƽ�ƣ�����G����Aʱֹͣ�˶���ͬʱ��PҲ�ӵ�A��������ÿ��3����λ���ٶ�������AD��DC�����˶��������Cʱֹͣ�˶������˶���ʱ��Ϊt. �ij��ȣ�
�ij��ȣ�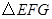 ƽ�ƵĹ����У���
ƽ�ƵĹ����У���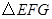 ��
��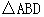 ��ص������Ϊ
��ص������Ϊ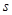 ,��ֱ��д�����
,��ֱ��д�����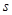 ���˶�ʱ��
���˶�ʱ��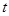 �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д��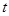 ��ȡֵ��Χ��
��ȡֵ��Χ��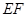 ���߶�
���߶�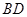 ���ڵ�
���ڵ� ������
������ .�Ƿ����������ʱ��
.�Ƿ����������ʱ��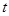 ��ʹ��
��ʹ��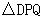 Ϊ���������Σ������ڣ������Ӧ��
Ϊ���������Σ������ڣ������Ӧ��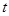 ֵ���������ڣ���˵������.
ֵ���������ڣ���˵������.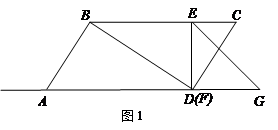
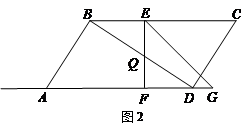
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 �£�
�£�
 D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com