
分析 (1)先化简二次根式、同时根据平方差公式计算乘法,再合并同类二次根式可得;
(2)将原式变形成符合平方差公式的形式,再先后利用平方差公式和完全平方公式计算可得.
解答 解:(1)原式=2$\sqrt{3}$-$\sqrt{3}$-1
=$\sqrt{3}$-1;
(2)原式=[$\sqrt{2}$+($\sqrt{3}$-$\sqrt{6}$)]×[$\sqrt{2}$-($\sqrt{3}$-$\sqrt{6}$)]
=2-($\sqrt{3}$-$\sqrt{6}$)2
=2-(3-6$\sqrt{2}$+6)
=2-3+6$\sqrt{2}$-6
=6$\sqrt{2}$-7.
点评 本题主要考查二次根式的混合运算,熟练掌握二次根式的混合运算法则及平方差公式、完全平方公式是解题关键.


科目:初中数学 来源: 题型:解答题
 有一组邻边相等,且另外两边也相等的四边形我们把它叫做筝形,如图1,四边形ABCD中,AD=DC,AB=BC,那么四边形ACBD叫做筝形.
有一组邻边相等,且另外两边也相等的四边形我们把它叫做筝形,如图1,四边形ABCD中,AD=DC,AB=BC,那么四边形ACBD叫做筝形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
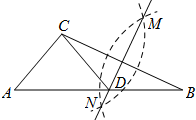 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为105°.
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为105°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com