
【题目】观察下列式子,并完成后面的问题
![]()
![]()
![]()
(1)![]()
(2)![]() .
.
你能利用上述关系式计算![]()
(3)利用(1)、(2)得到的结论,计算![]() 等于多少?并写出你是怎样得到的
等于多少?并写出你是怎样得到的
【答案】(1)![]() ;(2)24200;(3)19747,见解析
;(2)24200;(3)19747,见解析
【解析】
(1)观察不难发现,从1开始的连续自然数的立方和等于自然数的个数的平方乘比个数大1的数的平方,再除以4;
(2)将原式变形为(2×1)3+(2×2)3+(2×3)3+(2×4)3+…+(2×10)3=8×(13+23+33+43+…+103),再套用(1)中公式计算可得;
(3)由(1)得13+23+33+43+…+203=![]() ×202×212=44100,由(2)得23+43+63+83+…+203=8×
×202×212=44100,由(2)得23+43+63+83+…+203=8×![]() ×102×112=24200,两式相减从而得出13+33+53+73+…+193,再减去13+33+53,即可得答案.
×102×112=24200,两式相减从而得出13+33+53+73+…+193,再减去13+33+53,即可得答案.
解:(1)∵13=![]() ×12×22,
×12×22,
13+23=![]() ×22×32,
×22×32,
13+23+33=![]() ×32×42,
×32×42,
∴13+23+33+…+(n-1)3+n3=![]() ×n2×(n+1)2;
×n2×(n+1)2;
(2)原式=(2×1)3+(2×2)3+(2×3)3+(2×4)3+…+(2×10)3
=8×(13+23+33+43+…+103)
=8×![]() ×102×112
×102×112
=24200;
(3)由(1)知13+23+33+43+…+203=![]() ×202×212=44100,
×202×212=44100,
由(2)知,23+43+63+83+…+203=8×![]() ×102×112=24200,
×102×112=24200,
∴13+33+53+73+…+193=44100-24200=19900,
又∵13+33+53=1+27+125=153,
∴73+93+…+193=19900![]() 19747.
19747.


科目:初中数学 来源: 题型:
【题目】已知![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两个实数根.
的两个实数根.
(1)是否存在实数k,使![]() 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.
(2)求使![]() 的值为整数的实数k的整数值.
的值为整数的实数k的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师给出了如下问题:

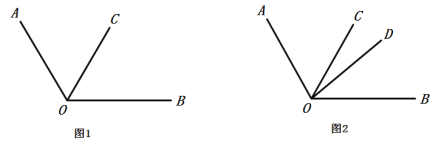
(1)以下是小刚的解答过程,请你将解答过程补充完整:
解:如图2,因为![]() ,
,![]() 平分
平分![]() ,
,
所以![]() ______
______![]() ______
______![]() (角平分线的定义).
(角平分线的定义).
因为![]() ,
,
所以![]() ______
______![]() .
.
(2)小戴说:“我觉得这道题有两种情况,小刚考虑的是![]() 在
在![]() 内部的情况,事实上,
内部的情况,事实上,![]() 还可能在
还可能在![]() 的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出
的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出![]() 的度数:______.
的度数:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
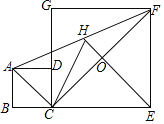
【题目】如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.
(1)求证:HC=HF.
(2)求HE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,M、N分别是线段AC、BC的中点,
![]()
(1)若AC=7cm,BC=5cm,求线段MN的长;
(2)若AB=a,点C为线段AB上任意一点,你能用含a的代数式表示MN的长度吗?若能,请写出结果与过程,若不能,请说明理由;
(3)若将(2)中“点C为线段AB上任意一点”改为“点C为直线AB上任意一点”,其余条件不变,(2)中的结论是否仍然成立?请画图并写出说明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
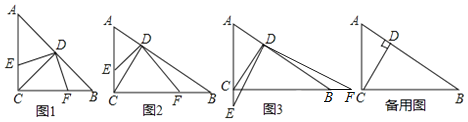
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点D,点E是直线AC上一动点,连接DE,过点D作
于点D,点E是直线AC上一动点,连接DE,过点D作![]() ,交直线BC于点F.
,交直线BC于点F.
![]() 探究发现:
探究发现:
如图1,若![]() ,点E在线段AC上,则
,点E在线段AC上,则![]() ______;
______;
![]() 数学思考:
数学思考:
![]() 如图2,若点E在线段AC上,则
如图2,若点E在线段AC上,则![]() ______
______![]() 用含m,n的代数式表示
用含m,n的代数式表示![]() ;
;
![]() 当点E在直线AC上运动时,
当点E在直线AC上运动时,![]() 中的结论是否任然成立?请仅就图3的情形给出证明;
中的结论是否任然成立?请仅就图3的情形给出证明;
![]() 拓展应用:若
拓展应用:若![]() ,
,![]() ,
,![]() ,请直接写出CE的长.
,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
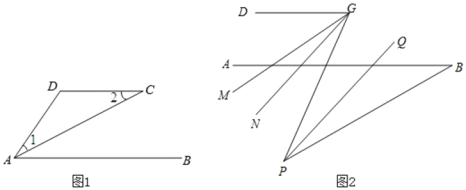
【题目】(1)如图1,AC平分DAB,12,试说明AB与CD的位置关系,并予以证明:
(2)如图2,在(1)的结论下,AB的下方点P满足ABP30,G是CD上任一点,PQ平分BPG,PQ∥GN,GM平分DGP,下列结论:
①DGPMGN的值不变;
②MGN的度数不变.
可以证明,只有一个是正确的,请你做出正确的选择并求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com