
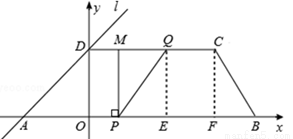
(2013年四川攀枝花12分)如图,在平面直角坐标系中,四边形ABCD是梯形,AB∥CD,点B(10,0),C(7,4).直线l经过A,D两点,且sin∠DAB=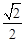 .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.

(1)点A的坐标为 ,直线l的解析式为 ;
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围;
(3)试求(2)中当t为何值时,S的值最大,并求出S的最大值;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
解:(1)(﹣4,0);y=x+4。
(2)在点P、Q运动的过程中:
①当0<t≤1时,如图1,
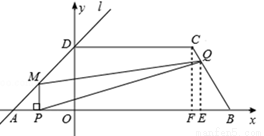
过点C作CF⊥x轴于点F,则CF=4,BF=3,由勾股定理得BC=5。
过点Q作QE⊥x轴于点E,则BE=BQ•cos∠CBF=5t•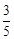 =3t。
=3t。
∴PE=PB﹣BE=(14﹣2t)﹣3t=14﹣5t,
S= PM•PE=
PM•PE= ×2t×(14﹣5t)=﹣5t2+14t。
×2t×(14﹣5t)=﹣5t2+14t。
②当1<t≤2时,如图2,
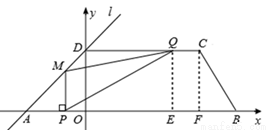
过点C、Q分别作x轴的垂线,垂足分别为F,E,则CQ=5t﹣5,PE=AF﹣AP﹣EF=11﹣2t﹣(5t﹣5)=16﹣7t。
S= PM•PE=
PM•PE= ×2t×(16﹣7t)=﹣7t2+16t。
×2t×(16﹣7t)=﹣7t2+16t。
③当点M与点Q相遇时,DM+CQ=CD=7,
即(2t﹣4)+(5t﹣5)=7,解得t=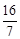 。
。
当2<t<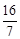 时,如图3,
时,如图3,
MQ=CD﹣DM﹣CQ=7﹣(2t﹣4)﹣(5t﹣5)=16﹣7t,
S= PM•MQ=
PM•MQ= ×4×(16﹣7t)=﹣14t+32。
×4×(16﹣7t)=﹣14t+32。
综上所述,点Q与点M相遇前S与t的函数关系式为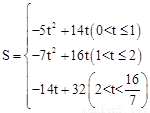 。
。
(3)①当0<t≤1时, ,
,
∵a=﹣5<0,抛物线开口向下,对称轴为直线t=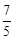 ,
,
∴当0<t≤1时,S随t的增大而增大。
∴当t=1时,S有最大值,最大值为9。
②当1<t≤2时,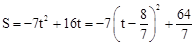 ,
,
∵a=﹣7<0,抛物线开口向下,对称轴为直线t=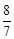 ,
,
∴当t=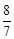 时,S有最大值,最大值为
时,S有最大值,最大值为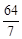 。
。
③当2<t<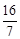 时,S=﹣14t+32
时,S=﹣14t+32
∵k=﹣14<0,∴S随t的增大而减小。
又∵当t=2时,S=4;当t=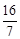 时,S=0,∴0<S<4。
时,S=0,∴0<S<4。
综上所述,当t=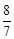 时,S有最大值,最大值为
时,S有最大值,最大值为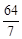 。
。
(4)t=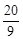 或t=
或t=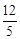 时,△QMN为等腰三角形。
时,△QMN为等腰三角形。
【解析】(1)利用梯形性质确定点D的坐标,由sin∠DAB=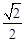 ,利用特殊三角函数值,得到△AOD为等腰直角三角形,从而得到点A的坐标;由点A、点D的坐标,利用待定系数法求出直线l的解析式:
,利用特殊三角函数值,得到△AOD为等腰直角三角形,从而得到点A的坐标;由点A、点D的坐标,利用待定系数法求出直线l的解析式:
∵C(7,4),AB∥CD,∴D(0,4)。
∵sin∠DAB=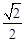 ,∴∠DAB=45°。∴OA=OD=4。∴A(﹣4,0)。
,∴∠DAB=45°。∴OA=OD=4。∴A(﹣4,0)。
设直线l的解析式为:y=kx+b,则有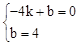 ,解得:
,解得: 。∴y=x+4。
。∴y=x+4。
∴点A坐标为(﹣4,0),直线l的解析式为:y=x+4。
(2)弄清动点的运动过程分别求解:①当0<t≤1时,如图1;②当1<t≤2时,如图2;③当2<t<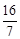 时,如图3。
时,如图3。
(3)根据(2)中求出的S表达式与取值范围,逐一讨论计算,最终确定S的最大值。
(4)△QMN为等腰三角形的情形有两种,需要分类讨论:
①如图4,点M在线段CD上,
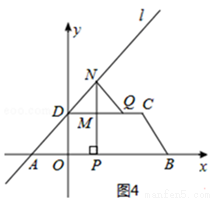
MQ=CD﹣DM﹣CQ=7﹣(2t﹣4)﹣(5t﹣5)=16﹣7t,MN=DM=2t﹣4,
由MN=MQ,得16﹣7t=2t﹣4,解得t=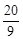 。
。
②如图5,当点M运动到C点,同时当Q刚好运动至终点D,
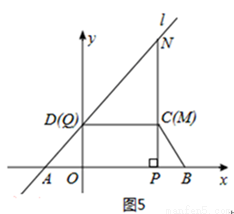
此时△QMN为等腰三角形,t=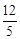 。
。
∴当t=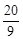 或t=
或t=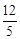 时,△QMN为等腰三角形。
时,△QMN为等腰三角形。
考点:一次函数综合题,双动点问题,梯形的性质,锐角三角函数定义,特殊角的三角函数值,由实际问题列函数关系式,一次函数和二次函数的性质,等腰三角形的性质,分类思想的应用。


科目:初中数学 来源:2013年初中毕业升学考试(四川攀枝花卷)数学(解析版) 题型:解答题
(2013年四川攀枝花8分)如图,PA为⊙O的切线,A为切点,直线PO交⊙O与点E,F过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交与点C,连接AC,BF.

(1)求证:PB与⊙O相切;
(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;
(3)若AC=12,tan∠F= ,求cos∠ACB的值.
,求cos∠ACB的值.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川攀枝花卷)数学(解析版) 题型:填空题
(2013年四川攀枝花4分)某次数学测验中,某班六位同学的成绩分别是:86,79,81,86,90,84,这组数据的众数是 ,中位数是 .
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川攀枝花卷)数学(解析版) 题型:选择题
(2013年四川攀枝花3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则函数 与y=bx+c在同一直角坐标系内的大致图象是【
】
与y=bx+c在同一直角坐标系内的大致图象是【
】
 A.
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川攀枝花卷)数学(解析版) 题型:选择题
(2013年四川攀枝花3分)已知实数x,y,m满足 ,且y为负数,则m的取值范围是【 】
,且y为负数,则m的取值范围是【 】
A.m>6 B.m<6 C.m>﹣6 D.m<﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com