练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，已知点O（0，0），A（3，0），点B在y轴正半轴上，且△OAB的面积为6，求点B的坐标及直线AB对应的函数关系式．

    【答案】y=﹣x+4，

    【解析】

    由于点B在y轴正半轴上，则B点的横坐标为0，只需求出B点的纵坐标即可．由△AOB的面积及OA的长，易求得B点纵坐标的绝对值，由此可得出B点的坐标

    解：设点B的坐标为（0，b）．

    ∵点O（0，0），A（3，0），

    ∴OA=3，

    ∵点B在y轴上，

    ∴△OAB是直角三角形，

    由题意得：S△OAB=×3×b=6，

    ∴b=4，

    即点B的坐标为（0，4），

    设直线AB的解析式为y=kx+4，

    把A（3，0）代入得：0=3k+4，

    解得，k=﹣，

    ∴直线AB的解析式为y=﹣x+4，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】
    （1）计算：|﹣ |+2﹣1+ （π﹣ ）0﹣tan60°；
    （2）解分式方程： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知含字母x，y的多项式是：3[x2+2（y2+xy﹣2）]﹣3（x2+2y2）﹣4（xy﹣x﹣1）

    （1）化简此多项式；

    （2）小红取x，y互为倒数的一对数值代入化简的多项式中，恰好计算得多项式的值等于0，那么小红所取的字母y的值等于多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（　　）
    A.2m3+3m2=5m5
    B.﹣5（﹣x3）﹣2=﹣
    C.（3a3b3）2=6a6b6
    D.
    =﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为25和17，则△EDF的面积为（　　）

    A. 4 B. 5 C. 5.5 D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，AD是高，E、F分别是AB、AC的中点，

    （1）AB＝10，AC＝8，求四边形AEDF的周长；

    （2）EF与AD有怎样的位置关系，证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上有A、B两点，A在B的左侧，已知点B对应的数为2，点A对应的数为a．

    （1）若a=﹣3，则线段AB的长为 （直接写出结果）；

    （2）若点C在线段AB之间，且AC﹣BC=2，求点C表示的数（用含a的式子表示）；

    （3）在（2）的条件下，点D是数轴上A点左侧一点，当AC=2AD，BD=4BC，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（12分）（1）如图1，在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM，垂足为M，且MN=DM．设OM=a，请你利用基本活动经验直接写出点N的坐标_____（用含a的代数式表示）；

    （2）如果（1）的条件去掉“且MN=DM”，加上“交∠CBE的平分线与点N”，如图2，求证：MD=MN．如何突破这种定势，获得问题的解决，请你写出你的证明过程．

    （3）如图3，请你继续探索：连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，请你指出正确的结论，并给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如：如图①，若点A，B在数轴上分别对应的数为a，b(a<b)，则AB的长度可以表示为AB=b－a．

    请你用以上知识解决问题：

    如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达A点，再向右移动3个单位长度到达B点，然后向右移动5个单位长度到达C点．

    （1）请你在图②的数轴上表示出A，B，C三点的位置．

    （2）若点A以每秒1个单位长度的速度向左移动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动，设移动时间为t秒．

    ①当t=2时，求AB和AC的长度；

    ②试探究：在移动过程中，3AC－4AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．

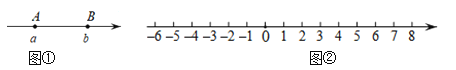
    查看答案和解析>>

    同步练习册答案